普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回のテーマは、「M-1グランプリの笑神籤(えみくじ)」です。
M-1ファイナリストのネタ披露順を決める運命のくじ引きを数学的に考えてみましょう!
M-1の運命を握る! 笑神籤(えみくじ)
漫才師の頂点を決める戦い「M-1グランプリ」。

毎年8月頃に1回戦がスタートし、年末に決勝戦がテレビ朝日系列で放送されます。
2021年のM-1グランプリエントリー数は、なんと6017組!ファイナリストは、敗者復活枠を含め、わずか10組です。長丁場の戦いを勝ち抜いてきた漫才師たちが決勝戦に賭ける意気込みは凄まじいものでしょう。
さらに、決勝戦も、一度の戦いでは済みません。ファーストラウンドと最終決戦の2部構成になっているのです。まず、全10組がファーストラウンドでネタを披露して、審査員により採点されます。そして、そのうちの上位3組が最終決戦に進み、ファーストラウンドとは異なるネタを披露して、審査員が「一番面白かった」と判断したファイナリストに投票することで、王者が決定するのです。
毎年、決勝戦では、さまざまなドラマが生まれます。
昨年は、ボケの長谷川雅紀さんと、ツッコミの渡辺隆さんのコンビ「錦鯉」が優勝し、大きな話題となりました。最終決戦の「逃げた猿を捕まえたい」というネタに、会場もお茶の間も大爆笑。そして、優勝が決まると、長谷川さんが大号泣。テレビを見ながら、もらい泣きしてしまった人も多いことでしょう。
そんな笑いあり涙ありの決勝戦。ファイナリストの運命を握るのは、審査員だけではありません。
決勝戦ファーストラウンドのネタ披露順を決定するくじ引き「笑神籤(えみくじ)」も、非常に重要な存在です。
笑神籤には、棒のようなものが10本入っており、それぞれにファイナリスト10組(敗者復活戦枠も含む)の名前が書かれています。これを順々に引いていき、ネタ披露順を決定していくのです。
しかも、一気に引くのではなく、1組ずつネタを披露するごとに引いていくので、出場者も視聴者もドキドキ。そして、この笑神籤が決めるネタ披露順が、ファイナリストの運命を左右していると指摘する人は少なくありません。
2021年決勝戦ファーストラウンド上位5組のネタ披露順を見てみましょう。
| 順位 | コンビ名 | 点数 | ネタ披露順 |
|---|---|---|---|
| 1位 | オズワルド | 665点 | 6番 |
| 2位 | 錦鯉 | 655点 | 8番 |
| 3位 | インディアンス | 655点 | 9番 |
| 4位 | ロングコートダディ | 649点 | 7番 |
| 5位 | もも | 645点 | 10番 |
※M-1グランプリ公式サイトによると、同点の場合は、”各審査員の得点を比較し、高得点をつけた審査員の人数が多い組を上位とする”というルールで順位を決定しているようです。
(引用元:M-1グランプリ公式サイト https://www.m-1gp.com/)
全組が後半にネタを披露していることがわかります。
前半も素晴らしいネタばかりで、私自身大笑いしながら見ていましたが、大会後半にかけて、なにかしら良い流れができていたのかもしれません。
ネタ披露順と結果の関係性についての分析は、お笑いの専門家の方たちにお任せすることにして……今回の記事では、「笑神籤が生み出すネタ披露順に関わる確率」を調べてみましょう!
10組のネタ披露順は何通り?
まずは、「10組のネタ披露順」が全何通りあるか調べてみます。
笑神籤の生み出す可能性は、果たして何通りあるのでしょうか?

10組で考えると、少し多いので、まずは「決勝に出場するのが3組だったら」というシチュエーションを想定してみましょう。
ファイナリスト3組の名前を「A,B,C」として、ネタ披露順を考えてみます。
例えば、1番目がAだとしましょう。すると、2番目にありうるのはBかCのいずれか2通りです。もしも、2番目がBになったら、3番目はCに決まります。同様にして、2番目がCになったら、3番目はBに決まります。
このように考えて、樹形図を描くと以下のようになります。
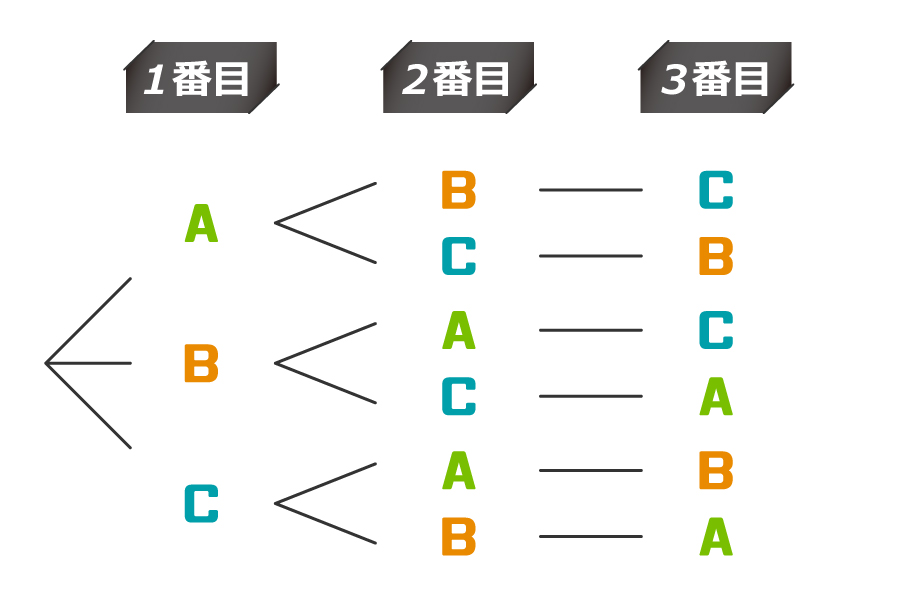
1番目の可能性は3通りで、その3通りそれぞれが2通りに分岐し、さらにその2通りそれぞれが1通りにつながっていく様子がわかりますね。
これを計算式で表現すると
\[
3\times 2\times 1=6
\]
となり、ネタ披露順は6通りであることがわかります。
この考え方は、「決勝に出場するのが4組だったら」というシチュエーションになっても同じです。
1番目の可能性は4通りで、その4通りそれぞれが3通りに分岐し、さらにその3通りそれぞれが2通りに分岐し、最後にその2通りそれぞれが1通りにつながっていきます。
これを計算式で表現すると
\[
4\times 3\times 2\times 1=24
\]
となり、ネタ披露順は24通りであることがわかります。
このように考えていくと、10組のネタ披露順を考える場合は
\[
10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1
\]
を計算すればよいことがわかります。
実際に計算してみると……なんと362万8800通り!
M-1決勝戦では、そのうちのたった1通りが、笑神籤によって決定されているのです。
つまり、確率は「362万8800分の1」。M-1決勝戦は、奇跡の時間であると言っても良いかもしれません。
また、数学では、今回出てきたような「数(正の整数)を1まで並べて、全部掛け合わせる」という計算に使える便利な記号があります。
例えば
\[
3!=3\times 2\times 1
\]
\[
10!=10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1
\]
というように、「!」を使って表現するのです。これは階乗と呼ばれていて、数学ではよく使います。
そして、この階乗は、記号の通り、びっくりするほど大きくなる性質を持っています。3の階乗は6でしたが、10の階乗は3628800、さらに20の階乗となると、なんと2432902008176640000となるのです!
順番が8番目になる確率は?
では次に、あなたがM-1決勝戦出場者だったとして、確率を考えてみましょう。
あなたは待合室で「何番目になるのかな?トップバッターだったら、どうしよう。8番目くらいが理想だなあ」などと考えながら、出番を待っているとします。
果たして、あなたのコンビは何番目になる確率が、最も高いのでしょうか?

1番目になる確率は、くじが10本ある状態から、あなたのコンビ名が書かれた1本を引き当てる確率なので、\(\frac{1}{10}\)となりますよね。
では、2番目になる確率はどうなるのでしょうか?あなた以外のファイナリストの名前が書かれたくじが1番目に引かれた後に、あなたのコンビ名が書かれたくじが2番目に引かれなければなりません。1番目になる確率を考えたときと比べ、複雑な状況となります。
3番目、4番目、5番目となると、さらに複雑になりそうですが……一体どうなるのでしょうか?
今回は「あなたのコンビが8番目になる確率」を例として考えてみましょう。
確率の分母は、順番の全パターンです。つまり、「10組のネタ披露順は全何通りあるか?」に対応するので、先ほど求めた\(10!= 3628800\)となります。
そして、確率の分子は、今回考えたいパターンである「あなたのコンビが8番目になるネタ披露順は何通りあるか?」に対応します。
これが、何通りになるかを調べてみましょう。
まずは「あなたのコンビが8番目になるネタ披露順」の具体例を見てみます。
あなたのコンビ以外の9組をA,B,C,D,E,F,G,H,Iとすると、
1番目: A
2番目: B
3番目: C
4番目: D
5番目: E
6番目: F
7番目: G
8番目: あなたのコンビ
9番目: H
10番目: I
や
1番目: C
2番目: B
3番目: A
4番目: H
5番目: I
6番目: D
7番目: F
8番目: あなたのコンビ
9番目: E
10番目: G
などが考えられますよね。
この例を見てわかる通り、「8番目があなたのコンビ」であることを固定しておけば、他9組はどんな順番に並べても構わないのです。
つまり
1番目: ?
2番目: ?
3番目: ?
4番目: ?
5番目: ?
6番目: ?
7番目: ?
8番目: あなたのコンビ
9番目: ?
10番目: ?
の9つの「?」の部分に、A~Iを自由に並べて入れていけばよいわけです。
つまり、「(あなたのコンビを除いた)9組のネタ披露順は全何通りあるか?」を計算すればよいことがわかります。
これは、「10組のネタ披露順は全何通りあるか?」と同様に考えられるので、\(9!\)通りとなります。
以上をまとめると、
・確率の分母は「10組のネタ披露順は全何通りあるか?」の\(10!\)
・確率の分子は「あなたのコンビが8番目になるネタ披露順は何通りあるか?」の\(9!\)
となるので、求めたい確率は
\begin{align*}
\frac{9!}{10!}&=\frac{9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}\\
&=\frac{1}{10}
\end{align*}
となります。トップバッターになる確率\(\frac{1}{10}\)と同じなんですね!
さらに、これは「8番目」に限らず、何番目であっても同じことが成り立ちます。
例えば、「あなたのコンビが3番目になるネタ披露順は何通りあるか?」についても、「3番目があなたのコンビ」であることを固定して、「(あなたのコンビを除いた)9組のネタ披露順は全何通りあるか?」を考えるので、同様の結果となるのです。
つまり、どの順番になるのかは全て確率\(\frac{1}{10}\)。トップバッターも3番目も8番目もラストも、どれも同じ確率なのです。
これには「くじ引きの公平性」というものが関わっています。
例えば、くじが100本で、当たりが3本であったとしましょう。引いたくじを元に戻すことなく、100人が一人ずつ順番にくじを引いていったとします。
このとき、何番目にくじを引いたとしても、当たりを引く確率は\(\frac{3}{100}\)となることが知られています。「残りものには福がある」とは言いますが、数学的には全て同じ確率なのです。
また、このようなくじ引きを考える際には、よく「条件付き確率」というものが使われます。確率に興味がある方は、調べてみてくださいね。
今回は、M-1の笑神籤をテーマにしましたが、その他にも日常のなかには「確率」を考えることができる対象がたくさんあります。「3人でじゃんけんをしたときに、あいこになる確率は?」「4桁の暗証番号が、日にちになる確率は?」など、考えてみると何か発見があるかもしれませんよ!
補足
本来であれば、「8番目に、あなたのコンビ名が書かれたくじが引かれる確率」を求める場合、「1~7番目にあなた以外のファイナリストの名前が書かれたくじが引かれ続け、かつ、8番目にあなたのコンビ名が書かれたくじが引かれる確率」を考え、計算していきます。そして、多くの場合、その際には「条件付き確率」を用います。今回は、わかりやすさを重視して、「ファイナリスト全10組を並べたときに、あなたのコンビが8番目になる確率」を考え、計算していきました。どちらも計算結果は同じとなります。
※参考文献
M-1グランプリ公式サイト(2022/2/7参照)
https://www.m-1gp.com/