地図がないとき、東京スカイツリー®までの距離を計算するには？　～役に立つ！三角比～

普段、私たちが見ているこの世界。

ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。

今回は、「もしも地図がなかったら……」という場面を考えていきます。

スマホがある今、「地図がない」という状況は考えづらいかもしれません。しかし、そんな不便な場面を想定してみると、数学が役立つことが見えてきます。

もしも地図がなかったら……

最近、地図を見る機会はありましたか？

コロナ禍で外出機会が減り、「地図を見る機会が減ったなあ」という人も多いかもしれません。

しかし、初めての場所に行くときなど、やはり地図は欠かせないものです。旅行先などでは、手放せない存在ですよね。

特に最近では、スマホの地図の便利さに驚かされます。

現在地を示し、ナビまでしてくれる……一昔前では考えられないほど高機能になっています。

当たり前に存在している上、どんどん便利になっている地図ですが、よくよく考えてみると「誰かがつくってくれたもの」ですよね。そして、大昔には「地図がなかった時代」もあったことでしょう。

そこで今回、試しに「もしも地図がなかったら……」というシチュエーションを想定してみたいと思います。

スカイツリーまでの距離は？

あなたは、地図がない状態で、東京を観光しているとします。すると、向こうの方に「東京スカイツリー」が見えました。

「せっかくなので、歩いてスカイツリーまで行こう！」と思ったのですが、地図がないため、ここからどのくらいの距離があるかわかりません。

もしも、かなりの距離を歩かなければならないとしたら、大変ですよね。スカイツリーは634メートルもあるので、近そうに見えて、案外すごく遠くにあるかもしれません。

地図なしで、大まかな距離を把握するには、どうしたら良いのでしょうか？

こんなときに、とても役に立つ情報が3つあります。

それは、「仰角（ぎょうかく）」「地面から目までの高さ」「三角形の比」です。これらがわかると、スカイツリーまでの距離を計算することができるのです。

まず、「仰角」とは、何かを調べてみると……

物を見上げたときの視線の方向と、水平面とのなす角

引用元Weblio辞書　デジタル大辞泉「仰角」

とのこと。天文学では「高度」とも呼ぶそうです。

今回のケースでは「スカイツリーのてっぺんを見上げたとき、あなたは視線の角度を、水平面からどのくらい上げたか？」に対応します。

つまり、下の図の角\(a\)が、仰角です。

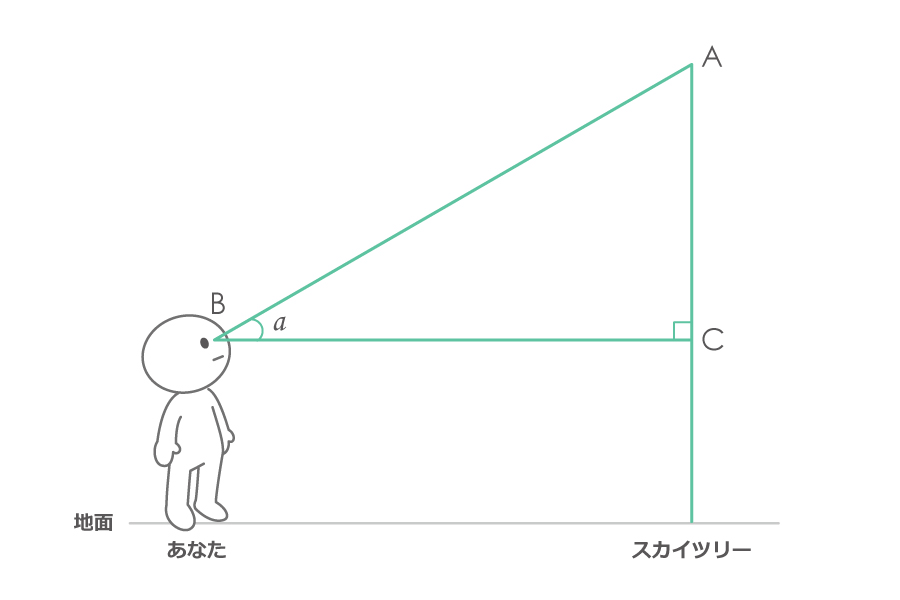
仰角をキッチリ正確に測るためには、精密な計測機器が必要になってくるでしょう。しかし、簡易的に大まかな角度を測る方法がいくつかあります。

なかでも、分度器や重りを使って、簡単な計測器をつくる方法が有名です。少し手間はかかりますが、工作好きの人であれば、楽しんでつくることができると思います。よかったら調べてみてくださいね！

また、星の観測では「げんこつ」などの手の形を使って仰角を測ることもあるそうです。以下のサイトでは、げんこつ1個が10°に相当することを使って、仰角を測る方法を紹介しています。

※NHK for School「げんこつを使った高度のはかり方」

今回のケースでは、仰角が30°であったとしましょう。

次に、調べるのは「地面から目までの高さ」です。

これは、おおよそ

「あなたの身長」-「あなたの目から頭のてっぺんまでの長さ」

に相当します。
※車椅子などを使用している場合は、この限りではありません。「身長」を「座った状態での自分の高さ」に変えて、計算する必要があります。

「あなたの目から頭のてっぺんまでの長さ」は、人によってさまざまではありますが、およそ10～15センチであると言われています。

したがって、

「あなたの身長」- 10センチ

を計算すると、大体の「地面から目までの高さ」が得られます。

もちろん、厳密には、この式では不正確で、靴の厚みなども考慮するべきです。本来であれば、精密な計測機器を使用して、きちんと測るべきでしょう。

しかし今回は、すぐにわかる情報で、大まかに計算することにします。

例えば、「あなたの身長」が170センチ、「あなたの目から頭のてっぺんまでの長さ」が10センチであるとしましょう。

すると、「地面から目までの高さ」は

170センチ – 10センチ = 160センチ

ということになります。

では、この二つの情報「仰角」と「地面から目までの高さ」を、図にあてはめてみます。

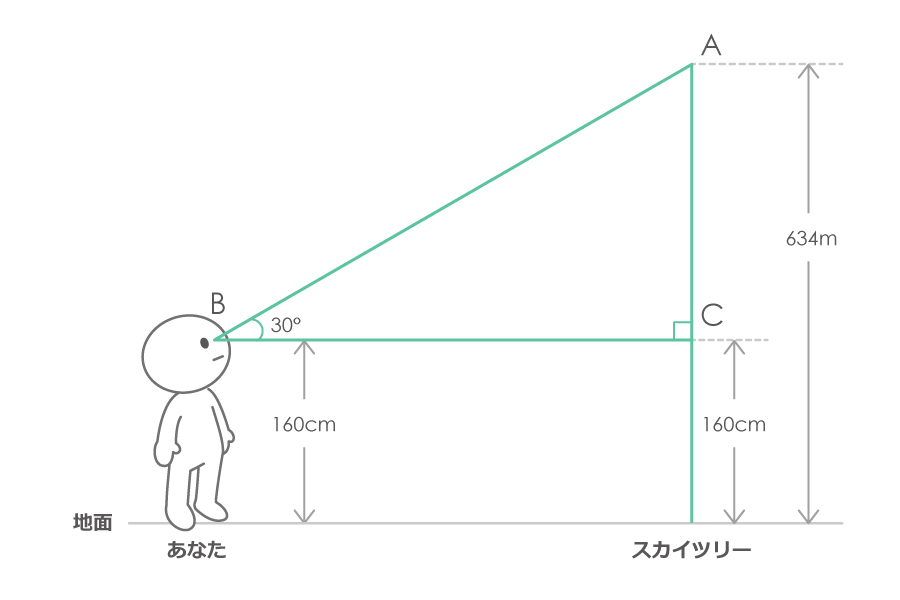
三角形ABCの高さ（辺AC）は

「スカイツリーの高さ」-「地面から目までの高さ」

なので、単位をメートルにして計算すると、

634メートル – 1.6メートル = 632.4メートル

です。

ここまでで、三角形ABCについて、かなり色々なことがわかってきましたね。

知りたかったのは「スカイツリーまでの距離」なので、三角形ABCの底辺（辺BC）がわかれば、見事解決となります。

最後に、もう一つの重要情報「三角形の比」を使って、仕上げとしましょう！

「三角形の比」で距離がわかる！

まずは、ここまでで得られた情報を、図にあてはめてみます。

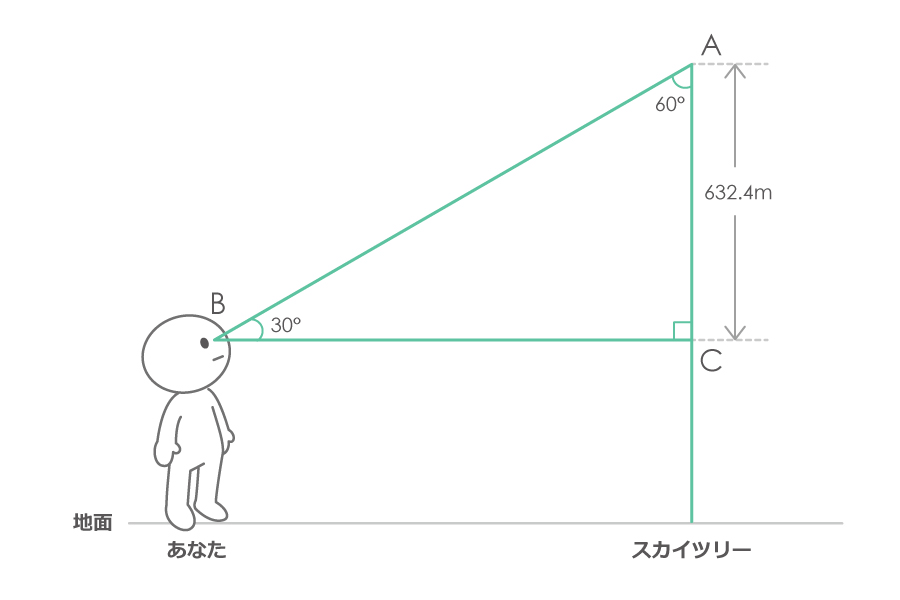
改めて、三角形ABCに注目してみましょう。

内角が「30°と60°と90°」ですよね。

この形状の直角三角形、どこかで見たことがありませんか？

正三角形を半分にした直角三角形です。三角定規の形状としても有名ですよね。

また、中学校では、辺の長さの比が「\(1:2:\sqrt{3}\)」と習った記憶があるのではないでしょうか。

つまり、三角形ABCの辺の長さの比は

\[
AC:AB:BC=1:2:\sqrt{3}
\]

となっているのです。

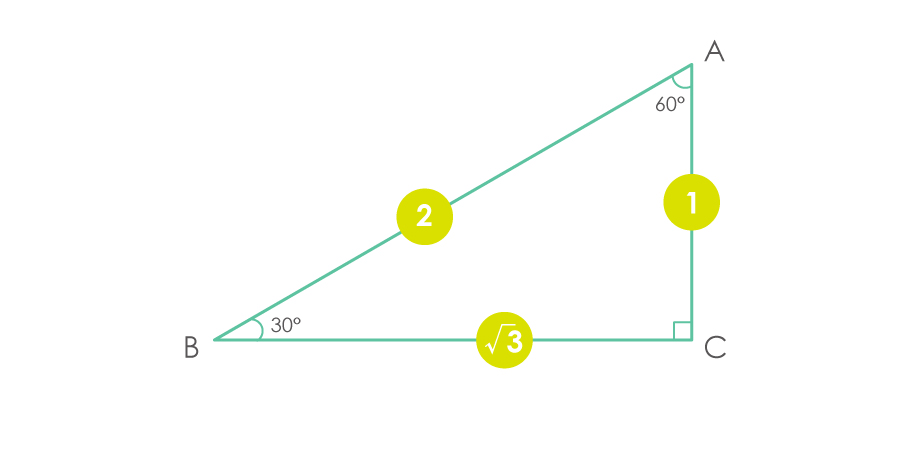
辺ACは、632.4メートルなので

\[
AC:BC=1:\sqrt{3}
\]

であることから、スカイツリーまでの距離（辺BC）は

\[
BC= AC \times \sqrt{3} = 632.4 \times \sqrt{3}
\]

となります。

\(\sqrt{3}\)の値は、およそ1.73です。中高生のときに「ひとなみにおごれや（1.7320508）」という語呂合わせで、\(\sqrt{3}\)の値を記憶した人もいるのではないでしょうか。

この値を使って計算してみると

\[
632.4 \times 1.73 = 1094.052
\]

となり、目標にしていた「スカイツリーまでの距離」が計算できました！

約1100メートル、つまり、約1.1キロメートルなので、およそ徒歩圏内であることが確認できましたね。

もちろん、歩く速度は人それぞれではありますが、そんなに無茶な距離ではなさそうです。

また、もしも「632.4×1.73を暗算するのはしんどい」と感じる人は、大きめに見積もって「650×2よりは小さい値になるから、1300メートルよりは小さいだろう」と計算してみるのもよいでしょう。

こんな風に考えてみると、地図なしでも、できることはたくさんあるんですね！

とても便利な「三角比」

今回のケース、実はちょっとズルいことをしています。

仰角が30°で、直角三角形ABCの内角が「30°と60°と90°」の有名な直角三角形だったため、辺の長さの比がすぐにわかってしまっていた点です。

もしも、三角形ABCが有名な直角三角形ではない場合はどうしたら良いのでしょうか？

たとえば、仰角が20°で、直角三角形ABCの内角が「20°と70°と90°」であった場合、どのように辺の長さの比を求めれば良いのでしょうか？