普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回は「アナログ時計にまつわる数学」を紹介します。
アナログ時計を観察してみると、不思議なことがたくさんあります。
例えば、1時間で長針が1周360°回転しますが……そういえば、どうして1周って360°なんでしょうね?
アナログ時計の不思議
今、あなたの近くにアナログ時計はありますか?

最近は、スマホやパソコンで時間を確認することが多いので、デジタル時計を使っている人の方が多いかもしれませんね。
とはいえ、職場やお店の掛け時計、腕時計など、様々な場面でアナログ時計を見かけます。円盤に書かれた1から12までの数字と針をパッと見て、時間をすぐに確認できるなんて、便利な道具ですよね。
そんなアナログ時計ですが、よくよく考えてみると、いくつか不思議なことがあります。
例えば、円盤に書かれた1から12までの数字。なんで「1から12」なんでしょうね?「1から10」の方が、キリが良い気がしませんか?
他にも、1時間経過すると、長針がぐるりと1周360°回転しますよね。なんで「1周は360°」なんでしょうね?「1周は100°」の方が、キリが良い気がしませんか?
さらに言えば、それぞれの数字の間は5等分されており、合計60分割で「60秒・60分」を表現していますよね。なんで「60秒・60分」なんでしょうね?これも「100秒・100分」の方が、キリが良い気がしませんか?
「円盤の数字は1~12、1周は360°、1分は60秒、1時間は60分」を「円盤の数字は1~10、1周は100°、1分は100秒、1時間は100分」とした方が、キリが良さそうなのに、なぜそうしないのでしょうか?
もしも1周を100°としたら…?
まずは「1周は360°」について考えてみることにしましょう。
「1周は360°」は人間が決めたルールのようなものです。そのため、これを変更して、思考実験しても何の問題もありません。
試しに「1周は100°」として、考えてみましょう。もしかしたら、360°よりも便利かもしれませんよね!
では、丸いピザを等分することを考えてみましょう。あなたは分度器(半周50°)を持っていて、きっちり角度を測って等分するとします。

もしも、2人でピザを分けるならば、「1周100°」を2等分するので「50°ずつ」に分けることになりますよね。
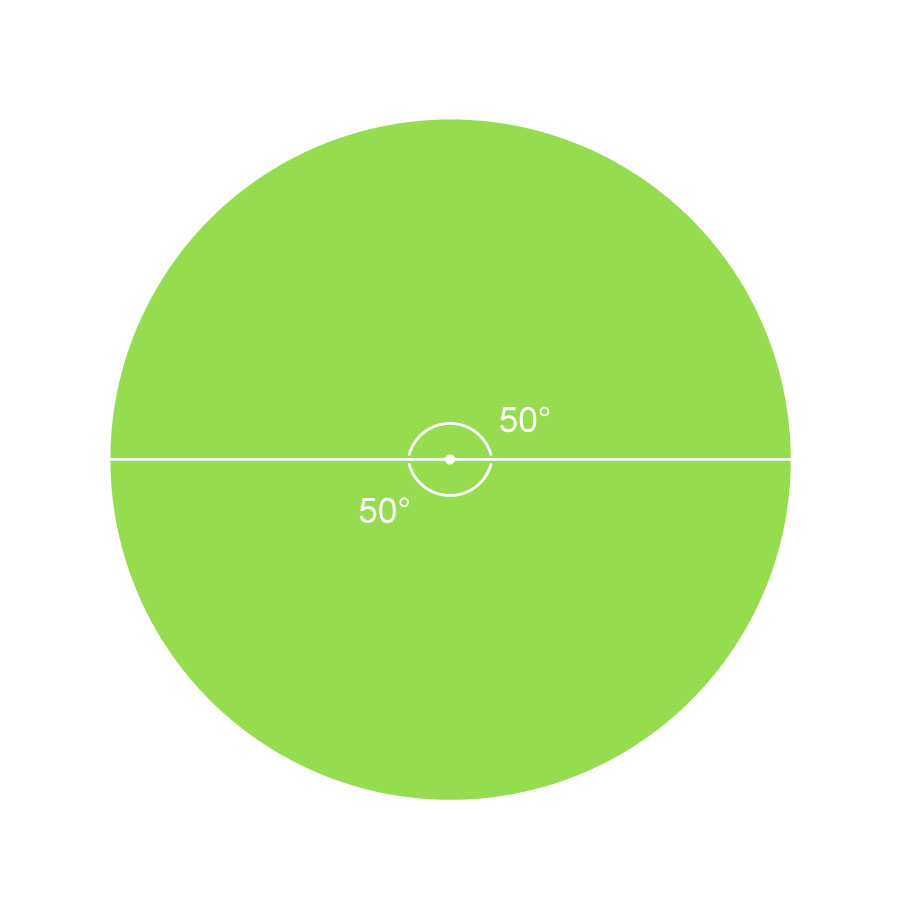
4人でピザを分けるならば、「1周100°」を4等分するので「25°ずつ」に分けることになりますよね。
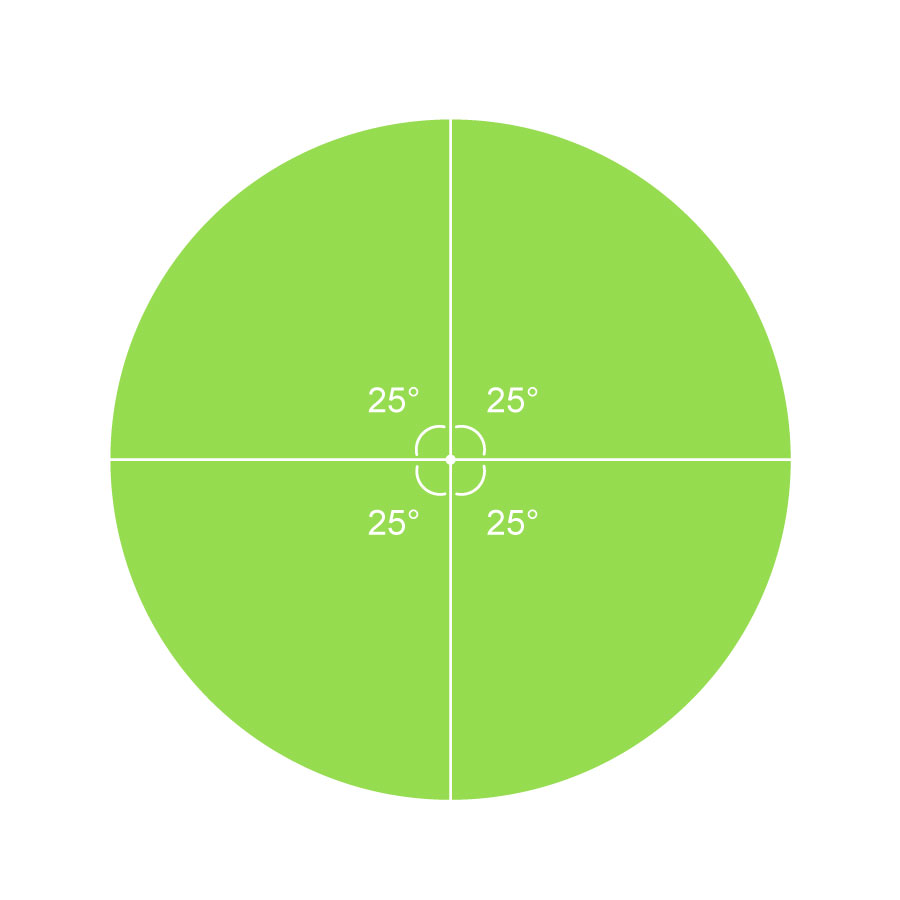
「\(100 \div 2\)」と「\(100 \div 4\)」、どちらも計算はとっても簡単。「1周100°」でも良さそうですね!
では、次に3人でピザを分けることを考えてみましょう。
すると、
\[
100 \div 3=33.3333333 \cdots
\]
となり、残念ながら、割り切れません。
つまり、分度器を使ってピザを3等分する場合、「33.333333…°」を測って分けることになります。これは困りましたね……。
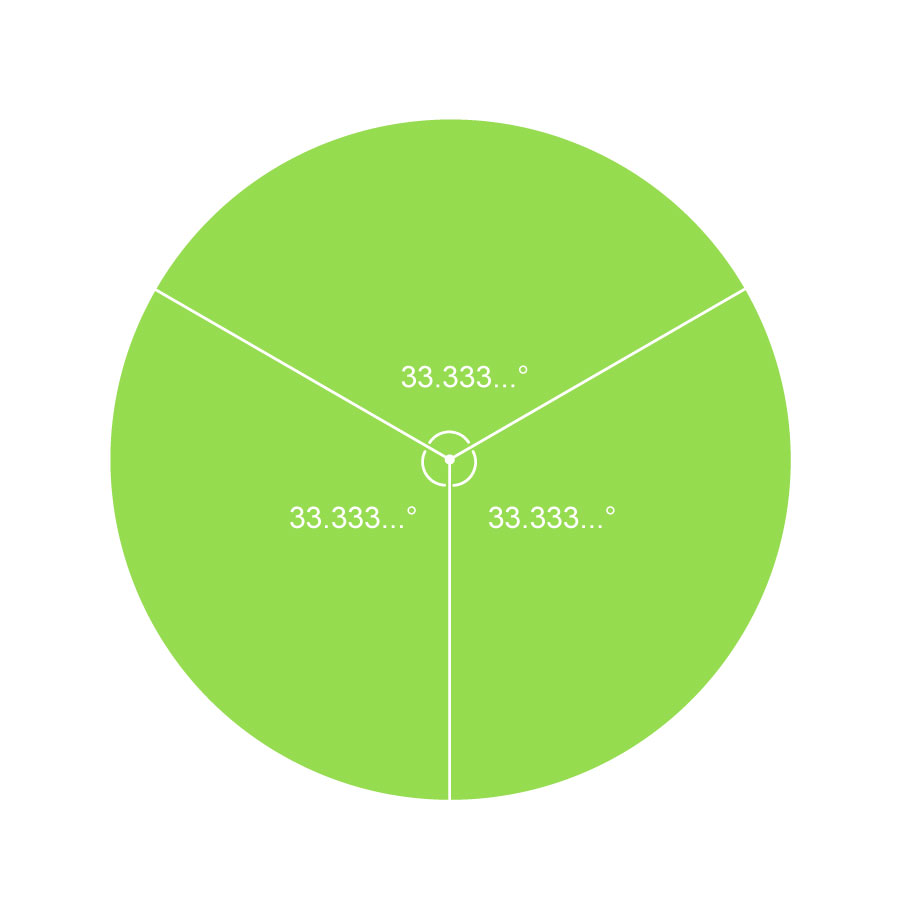
また、6等分の場合は「16.6666666…」、9等分の場合は「11.1111111…」を測ることになります。これらも、なかなか大変そうです。
それでは、「1周は360°」に戻して、同じことを考えてみましょう。
2等分: \(360 \div 2=180\)
3等分: \(360 \div 3=120\)
4等分: \(360 \div 4=90\)
6等分: \(360 \div 6=60\)
9等分: \(360 \div 9=40\)
となるので、どれもキッチリ割り切れています。こちらの方が分度器(半周180°)で測りやすいですね!
比較のため、100と360を2等分~10等分した数を書いた表を見てみましょう。
| 等分数 | 360 | 100 |
|---|---|---|
| 2等分 | 180 | 50 |
| 3等分 | 120 | 33.33333… |
| 4等分 | 90 | 25 |
| 5等分 | 72 | 20 |
| 6等分 | 60 | 16.66666… |
| 7等分 | 51.428571… | 14.285714… |
| 8等分 | 45 | 12.5 |
| 9等分 | 40 | 11.11111… |
| 10等分 | 36 | 10 |
100は「2, 4, 5, 10」の4個の数でしか割り切れていませんが、360は「2, 3, 4, 5, 6, 8, 9, 10」の8個の数で割り切れています。こんなにも差があるんですね!
ということは、「1周は360°」を採用した方が何かと便利そうです。
私たちの日常に溶け込んでいる「高度合成数」
突然ですが、小学校で習った「約数」を覚えていますか?
例えば、6の約数は「6を割り切る数(正の整数)」なので「1, 2, 3, 6」となります。7の約数は「1, 7」となり、10の約数は「1, 2, 5, 10」となります。
(※正の整数とは、1, 2, 3, 4, 5, …のような数のことです。6の約数を「6を割り切る整数」とすることもありますが、今回は正の整数に限定します)
この「約数」の個数が多いほど、割り切る数が多くなり、等分するときに便利な数となっているのです。
では、先ほど扱った100と360の約数をそれぞれ求めてみてください。ちょっと大きい数ですが、ぜひチャレンジしてみてくださいね!

100の約数は「1, 2, 4, 5, 10, 20, 25, 50, 100」の9個です。
360の約数は「1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360」の24個です。
3倍近い差がありますね!
「100よりも360の方が大きいから約数の個数が多いのかな」と思った方もいるかもしれませんが、大きさの違いだけが要因というわけではなさそうです。
例えば、350の約数は「1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350」の12個なので、360の約数の個数の半分しかありません。他にも、400の約数は「1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200, 400」の15個です。400の方が360より大きいのにも関わらず、360の約数の個数の方が多いですね。
どうやら360は、特別に約数の個数が多い数のようです。
実は、このような「約数の個数が多い数」を表す「高度合成数」というものがあります。
「高度合成数」とは「正の整数で、それ未満のどの正の整数よりも約数の個数が多いもの」のことです。ちょっと難しそうですが、具体例を見てみると、わかりやすいですよ。
例えば、1~12の約数の個数を表にして考えてみましょう。
| 正の整数 | 約数の個数 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 2 |
| 4 | 3 |
| 5 | 2 |
| 6 | 4 |
| 7 | 2 |
| 8 | 4 |
| 9 | 3 |
| 10 | 4 |
| 11 | 2 |
| 12 | 6 |
ここで、6に着目してみます。6未満の数である「1, 2, 3, 4, 5」の約数の個数は、それぞれ「1個、2個、2個、3個、2個」ですよね。そして、6の約数の個数は「4個」です。つまり、6の約数の個数は、自分より小さい1~5の約数の個数よりも多いことがわかります。
このような「自分より小さいどの数よりも約数の個数が多いもの」を「高度合成数」と呼びます。
上の表を見ながら、高度合成数を列挙してみると「1, 2, 4, 6, 12」が高度合成数であることがわかります。
さらに、大きな数まで調べて、高度合成数とその約数の個数を列挙してみると……
| 高度合成数 | 約数の個数 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 4 | 3 |
| 6 | 4 |
| 12 | 6 |
| 24 | 8 |
| 36 | 9 |
| 48 | 10 |
| 60 | 12 |
| 120 | 16 |
| 180 | 18 |
| 240 | 20 |
| 360 | 24 |
| 720 | 30 |
となります。
この表に書かれている高度合成数、「なんかよく見る数だなあ」と思いませんか?
例えば
12: アナログ時計に書かれた1~12の数字、1年は12ヶ月、1ダースは12個
24: 1日は24時間
60: 1分は60秒、1時間は60分
360: 1周は360°
ですよね。アナログ時計を観察しているときに出てきた「円盤の数字は1~12、1周は360°、1分は60秒、1時間は60分」の「12, 360, 60」は全て高度合成数なんですね!
このように、さりげなく高度合成数は日常に溶け込んでいます。そして、私たちは、これらの数の便利な性質の恩恵を、知らず知らずのうちに受けているのです。
例えば「四半期」も「12ヶ月を4等分すると3か月になる」からこそ成立しています。もしも、1年が10ヶ月だった場合、4等分すると2.5ヶ月となってしまいます。
他にも、お菓子が12個入りや24個入りであれば、家族や友人と等分しやすいですよね。2人でも3人でも4人でも6人でも、きっちり分けることができます。

こんな視点で、身の周りの数を眺めてみると、今まで気づかなかった発見が色々ありそうです。そういえば、干支の十二支や、大安や仏滅などの六曜も「12と6」で高度合成数ですね!
ぜひ、身近な「高度合成数」を探し出してみてくださいね。そこには何か秘密があるかも……。
補足
今回の記事は「高度合成数の利便性」を解説したものに過ぎません。時間や暦などにまつわる数字の採用理由には、さまざまな歴史的経緯が関わっているようです。
「1日はなぜ24時間で、時計は1周12時間なのか?」(2022/1/9参照)では、
(前略)古代バビロニアで暦や時間体系を決めるにあたっては、数学、天文学、占星術など当時のあらゆる学問、知識を総合的に考えて決定されたのでしょう。
と記載されています。