普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。

今回は「美しい数学の曲線」を紹介します。
実は、数式で表現される曲線とみなさんが日頃から見ている世界には、不思議な繋がりがあるのです。
「あれ、この曲線〇〇に見えるかも」なんて発見があるもしれませんね。

例えば、こんな数式で表現される曲線を描いていきます。

\[
r=1+\cos{\frac{7}{8}\theta}
\]

三角関数のコサインがあるし、何だか難しそうですね……。
でも、実際に曲線を描いてみるとビックリ！味わい深く、美しく、意外な形が見えてきます。

心臓の形をした曲線「カージオイド」

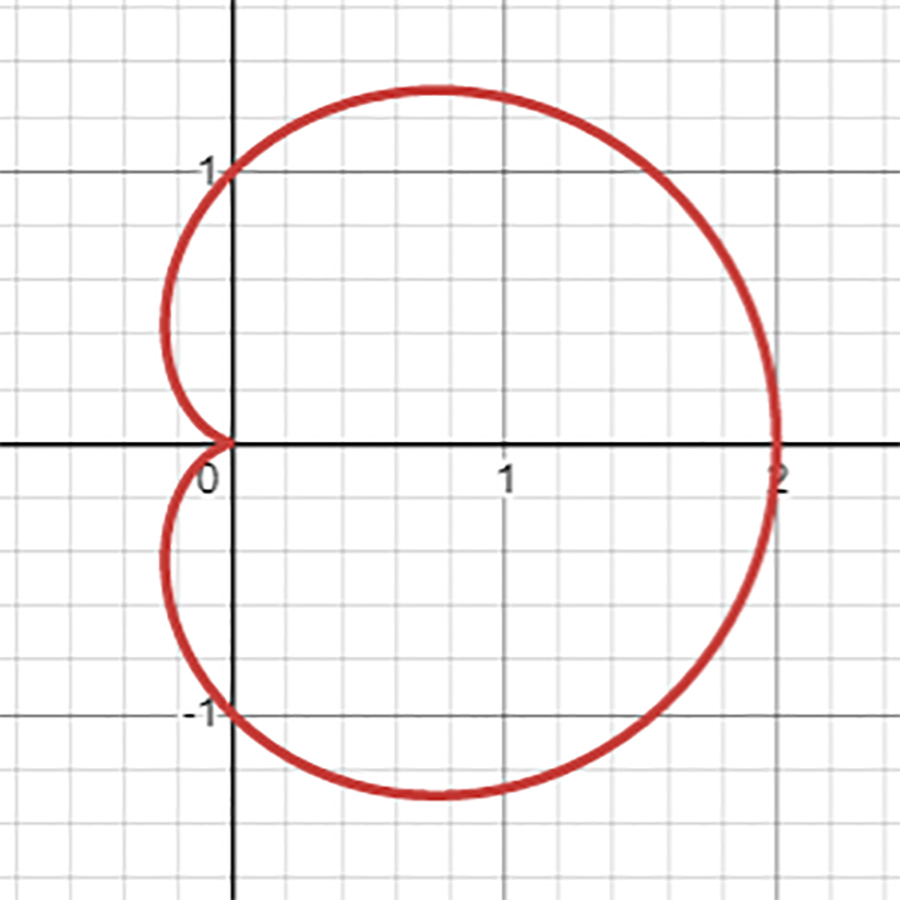
このなんともいえない可愛らしいフォルム。私にとって思い入れがある曲線なのです。

昔、数学の定期試験で、こんな問題が第一問として出題されました。

以下の極方程式で表されるグラフの概形を描け。

\[
r=1+\cos{\theta} \quad (0\leq \theta \leq 2\pi)
\]

連日の試験勉強で疲れ切っていた私。なんとか力を振り絞って計算し、グラフの形を探っていきました。
「ここでこんな風に曲がって、ここではこう下がって…」と、頭の中で独り言を呟きながら、グラフを描いてみると…

「ハート型みたいになった！」と、思わずホッコリ。
試験勉強の疲れが一気に吹っ飛んでしまいました。

この曲線は「カージオイド」と呼ばれ、日本語では「心臓形」とも呼ばれている有名な曲線です。

カージオイド自体も興味深い曲線ではありますが、以前、ある人から「カージオイドを表現する数式を少し変えながら曲線を描くと、面白いことが起こる」と教えてもらいました。

では、この「丸っこいハート型の曲線　カージオイド」をヒントに、遊んでみましょう！

心臓形が花の形に

カージオイドを表現する数式は

\[
r=1+\cos{\theta}
\]

でしたが、これを少し変えてみましょう。

\[
r=1+\cos{2\theta}
\]

として、\(\theta\)を\(2\theta\)に変え、グラフ描画ツールを用いて曲線を描いてみます。

すると…

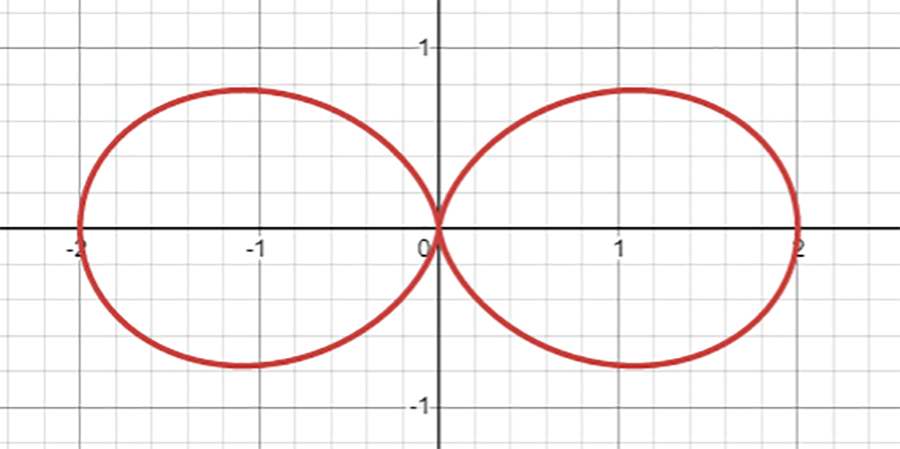
∞（無限大）のような形になりました。メガネや、リボンにも見えますね。

では、次に

\[
r=1+\cos{3\theta}
\]

として、\(\theta\)を\(3\theta\)に変えてみます。すると……

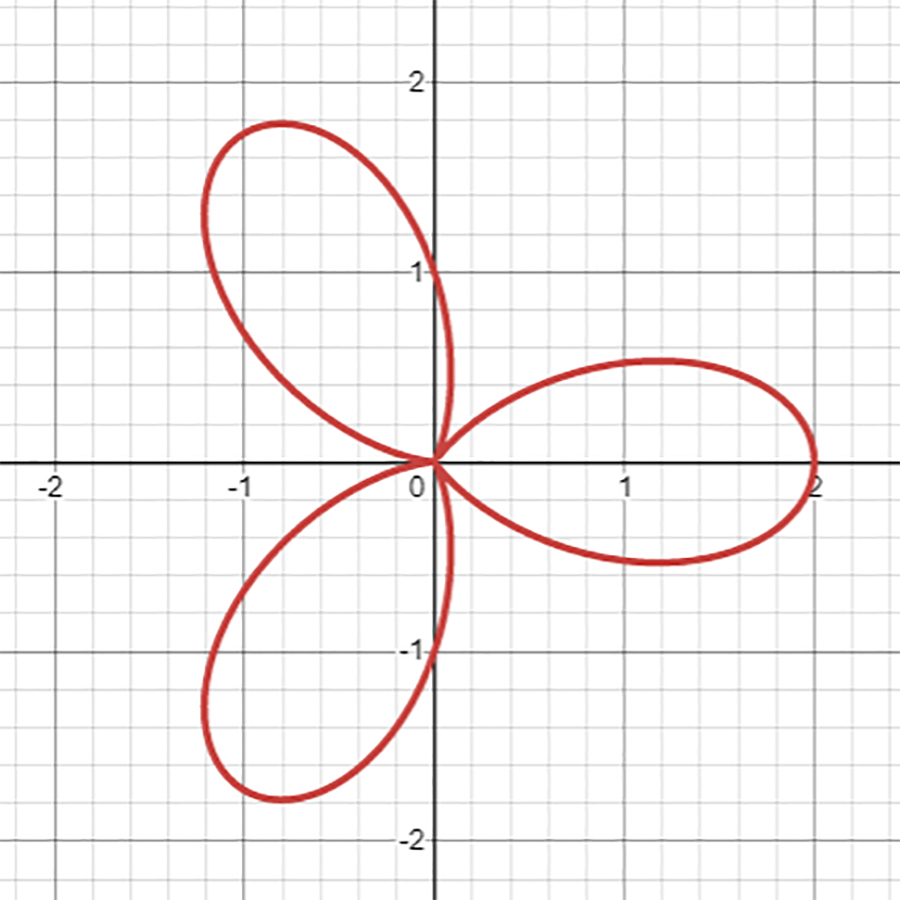
まるで花びらのようになりましたね。

\[
r=1+\cos{4\theta}
\]

にしてみると……

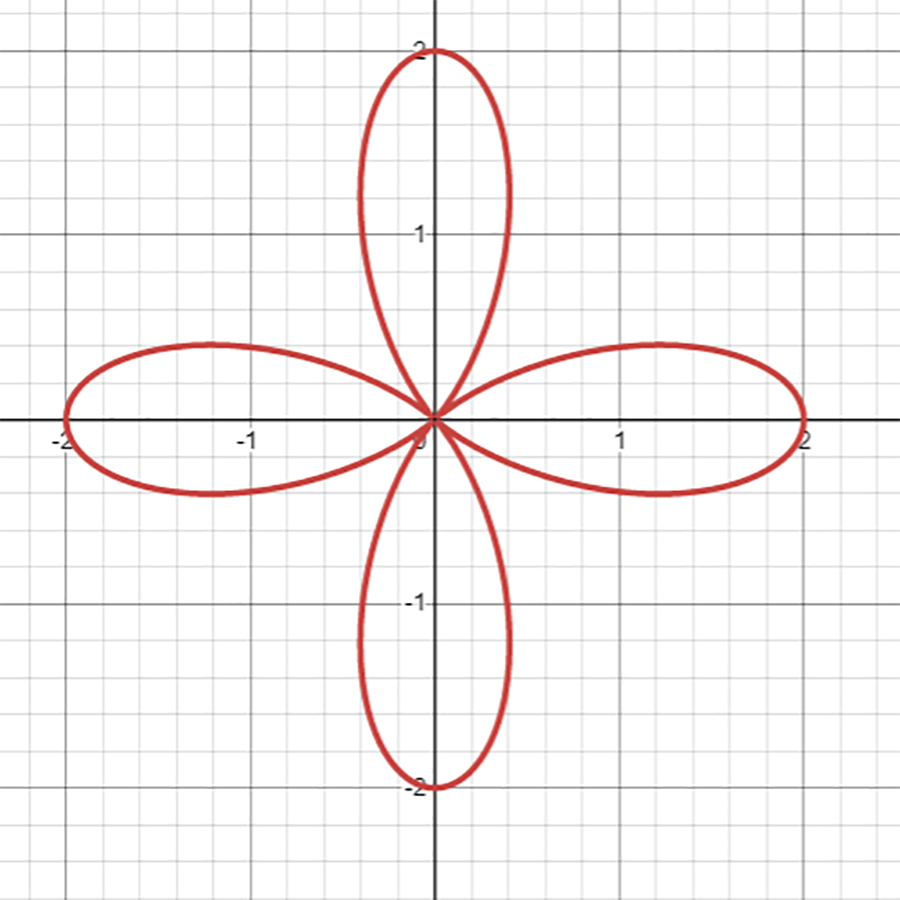
花びらが4枚になりました！

\[
r=1+\cos{5\theta}
\]

にしてみると……

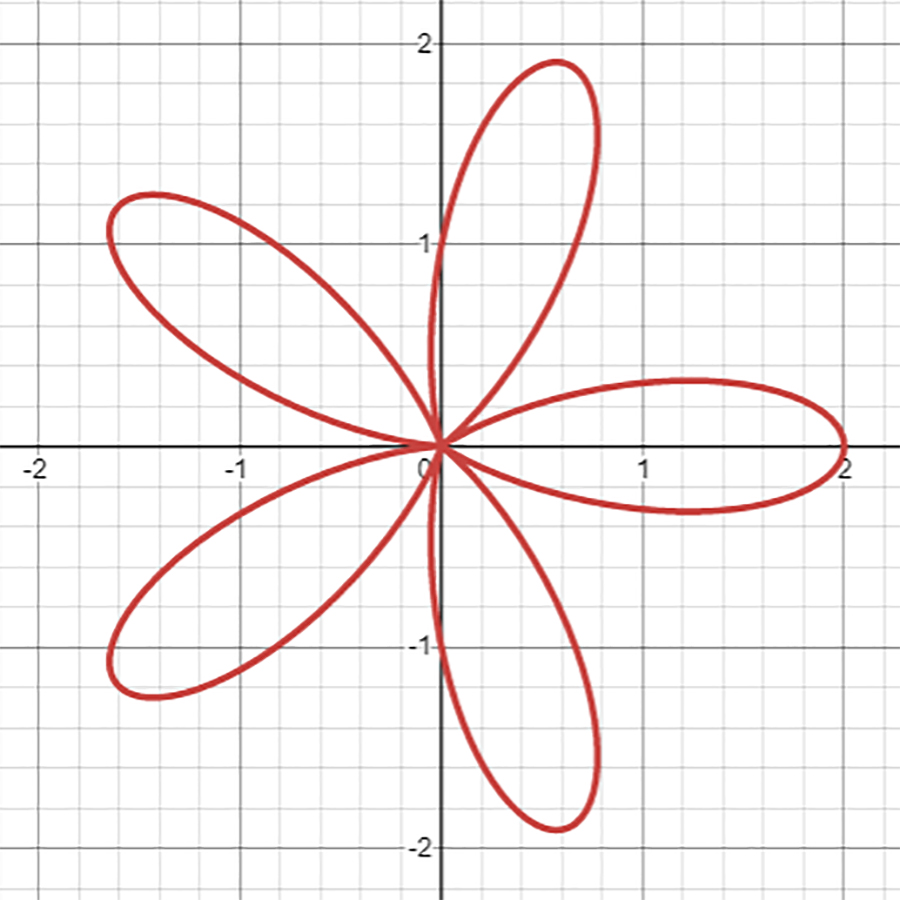
花びらが5枚に！

こんな風に心臓形が、花の形になっていくのです！

では、最後に

\[
r=1+\cos{\frac{7}{8}\theta}
\]

として、\(\theta\)を\(\frac{7}{8}\theta\)変えてみます。すると……

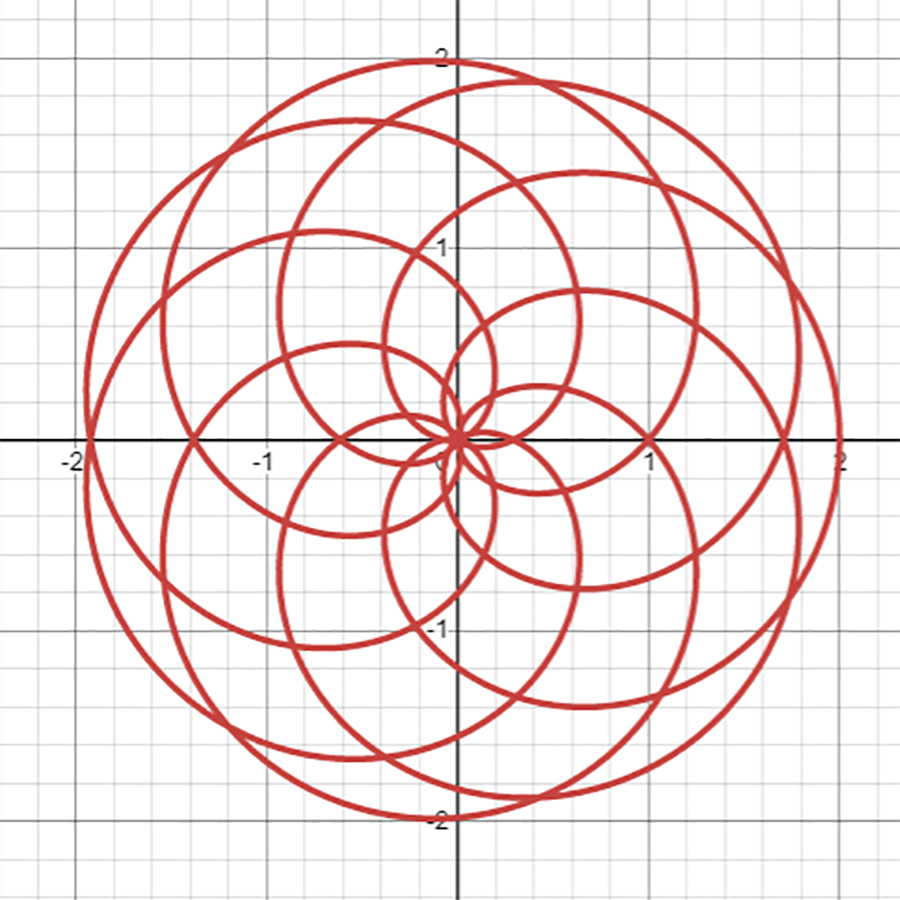
まるでバラを彷彿とさせる美しい曲線が現れました！

心臓形から、こんな曲線ができるなんて。想像がつきませんよね……。

波が織りなす「リサジュ―曲線」

では、次に、花の曲線たちとは趣の違う曲線たちを見ていきましょう。波が組み合わさってできる「リサジュ―曲線」です。

その姿は独特で面白味があり、電気通信大学の校章やマサチューセッツ工科大学のリンカーン研究所のロゴマークにも採用されているのです。

波の組み合わせ方により、様々な形が現れます。その姿をいくつか見てみましょう！

まず

\begin{align*}
x &= \sin{2\theta}\\
y &= \sin{3\theta}
\end{align*}

という数式で表現されるリサジュ―曲線を描いてみます。すると……

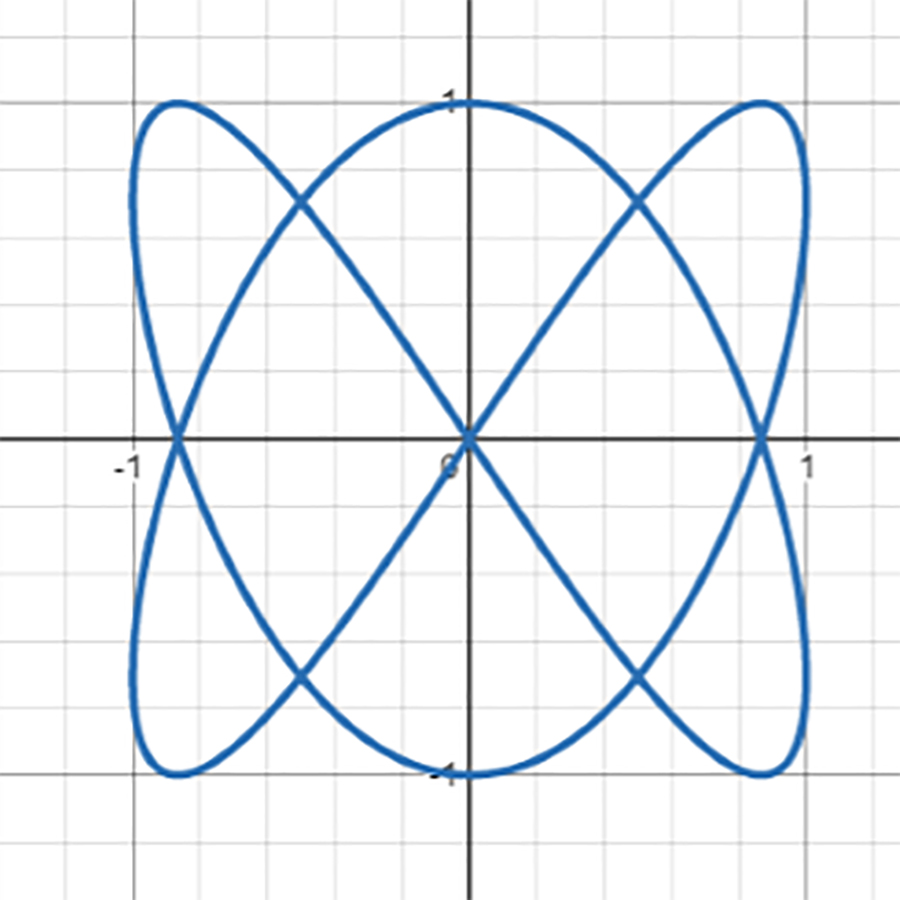
まるで何かの軌道のようですね！縄跳びのロープの動きのようにも見えます。

では、先ほどの数式を少しずつ変えながら、様々なリサジュ―曲線を見てみましょう！

\begin{align*}
x &= \sin{3\theta}\\
y &= \sin{4\theta}
\end{align*}

として、リサジュ―曲線を描いてみます。すると……

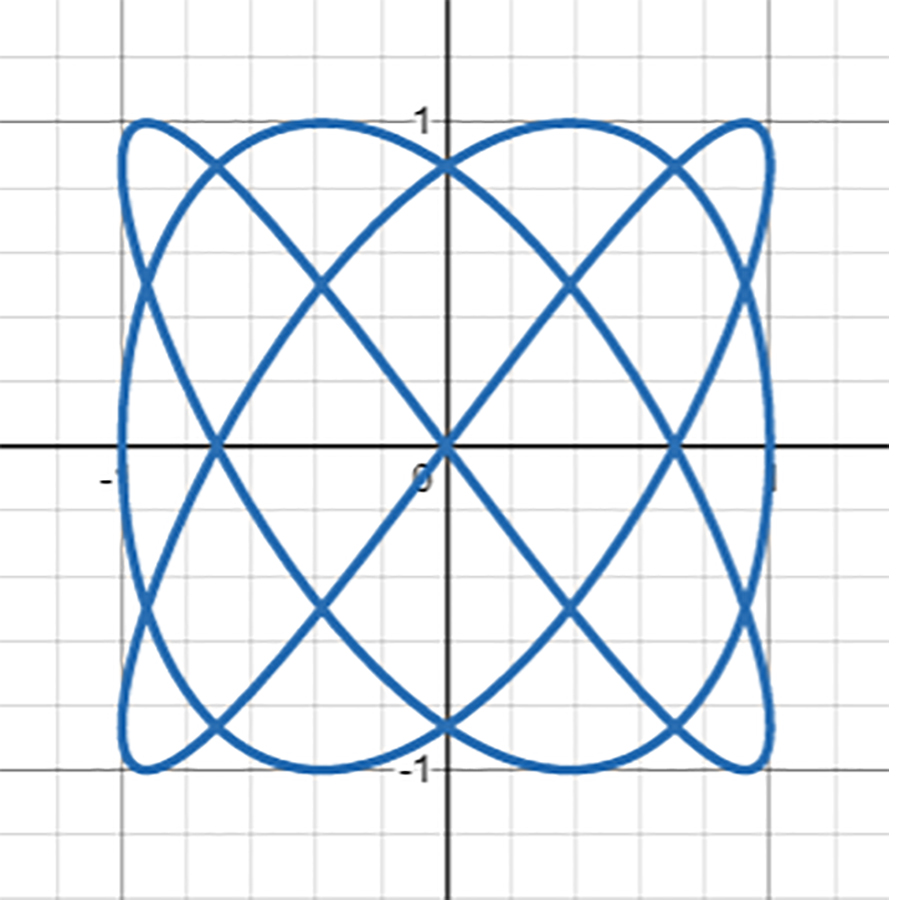
2次元ながらも、浮き出てくるように立体的になりました！

今度は、

\begin{align*}
x &= \sin{5\theta}\\
y &= \sin{4\theta}
\end{align*}

として、リサジュ―曲線を描いてみると……

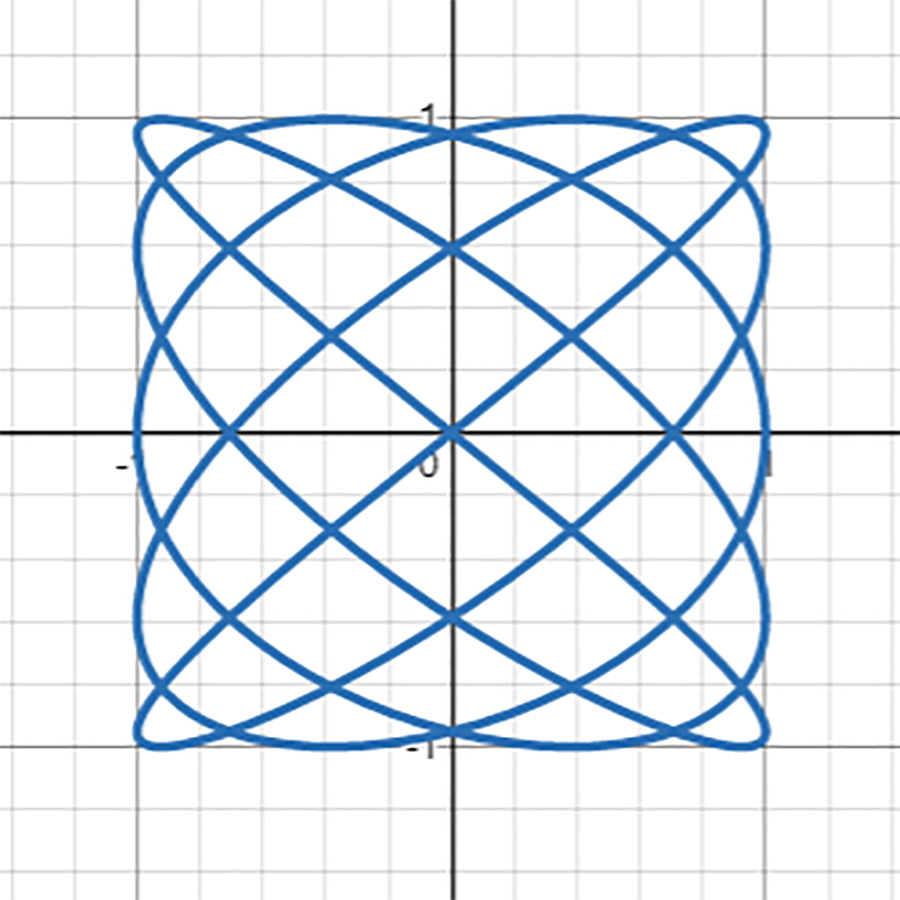
さらに、うねりが激しくなりましたね！

では最後に、

\begin{align*}
x &= \sin{7\theta}\\
y &= \sin{8\theta}
\end{align*}

として、曲線を描いてみると……

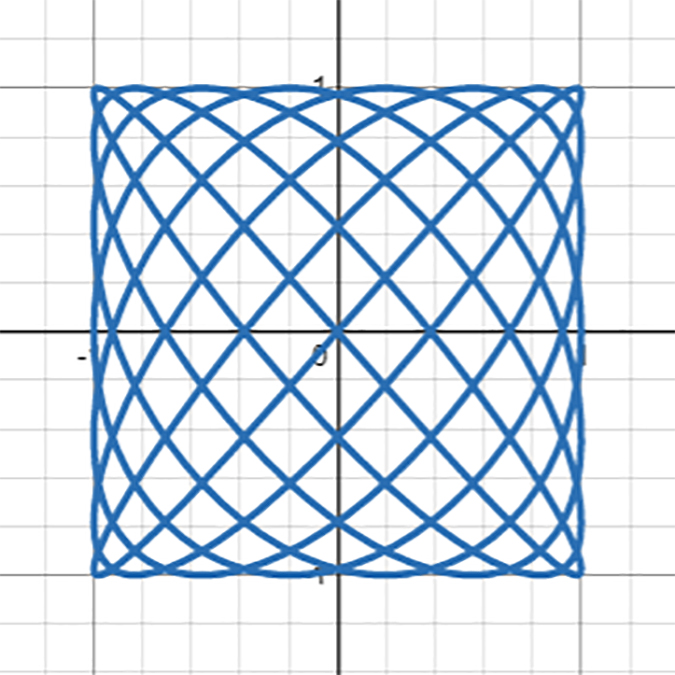
網目が細かくなり、より立体感のある形になりました！籠のようにも見えますね。

このリサジュ―曲線、その面白さは形状だけではありません。

オシロスコープという、時間経過とともに電気信号が変化していく様子を波形として映し出す測定器で、リサジュ―曲線を表示することができるのです。

例えば、電気通信大学の校章にリサジュ―曲線が採用された背景として、以下のような説明が書かれています。

オシロスコープ上のリサジュ―図形表示は、正確な無線周波数測定に利用されてきました。このことから、無線とリサジュ―図形とは切っても切れない関係があります。

引用元　電気通信大学とリサジュ―図形とはどの様な関係？(2021/02/25参照)

工学的にも、深い意味があるんですね！

数学の曲線を描いてみよう！

カージオイドやリサジュ―曲線、実際に描いてみたくありませんか？

実は、簡単に描く方法があるんです。パソコンさえあれば、数学が苦手な人もできますよ！

今回、私は「Desmos」というオンライン上のグラフ描画ツールを使用しました。

上記サイトの左側にある数式を入力する欄に「r=1+costheta」と、タイピングしてみてください。カージオイドが描かれます。

もう一つ、簡単に曲線を描くことができるサイトを紹介します。「Wolfram|Alpha」というサイトです。

なんと、このサイトでは検索窓に数式を入力するだけで曲線を描いてくれるのです！

次のように入力すると、今回紹介した曲線たちを描くことができますよ。

カージオイド

r=1+cos(theta)

花のような曲線（花びら2枚～5枚）

r=1+cos(2theta)
r=1+cos(3theta)
r=1+cos(4theta)
r=1+cos(5theta)

バラのような曲線

r=1+cos(7theta/8)

リサジュ―曲線（計4種類）

(sin(2theta),sin(3theta))
(sin(3theta),sin(4theta))
(sin(5theta),sin(4theta))
(sin(7theta),sin(8theta))

また、これらのものを少し変えて曲線を描いてみると、新しい形状を発見できるかもしれません。例えば、「r=1+cos(theta/8)」や「(sin(3theta),sin(5theta))」なども、ぜひ入力してみてくださいね。

そして、実は、「Wolfram|Alpha」では、数式を入力しなくても、思いもよらない曲線を描くことができます。試しに、「panda curve」や「rabbit curve」などと検索窓に入力してみてください。とっても面白いことが起こりますよ！

もちろん、今回紹介したもの以外にも、数学の面白い曲線はまだまだあります。色々な曲線を描いて、お気に入りの曲線を探し当てましょう！

【記事内のグラフ描画に使用したサイト】
Desmos　https://www.desmos.com/calculator?lang=ja