普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回は「黄金比」について紹介します。
自然界からデザインにまで関わっていると言われる黄金比。その裏側にある魅惑的な数学に、少しずつ迫っていきましょう!
黄金比とは?
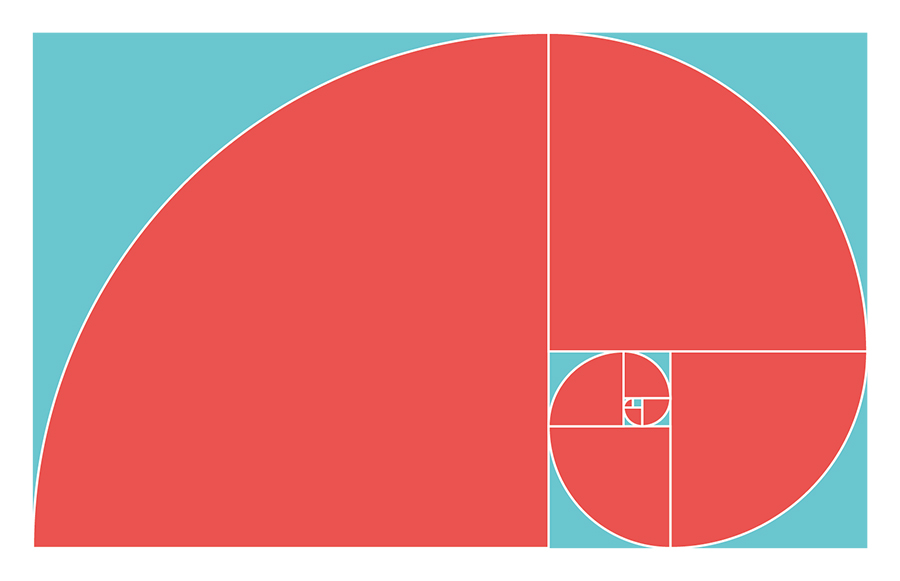
みなさんは、どのような場面で「黄金比」という言葉を聞いたことがありますか?何かとよく見聞きしますよね。
具体的にはWebサイトのデザインなど、日常の様々な場面で使われている比なんです。また、古代の芸術作品であるミロのヴィーナスからも黄金比を見出すことができると言われています。
まさに時間と空間を超えて、存在し続けている不思議な比。諸説ありますが、黄金比は「人間が美しく感じる比」であると言われています。
そんな神秘的な黄金比、具体的には
\[
1:\frac{1+\sqrt{5}}{2}
\]
という比です。
\(\sqrt{5}=2.2360679774 \cdots\)という値を入れて計算してみると…
\[
1: 1.6180339887 \cdots
\]
一見すると、かなり中途半端…。「1:1.5や1:2の方がキレイな感じがするなあ」と思う人もいるかもしれません。
しかし、実はこの
\[
1:\frac{1+\sqrt{5}}{2}
\]
という数の裏側には、とてもシンプルな2次方程式が隠されているのです。
それは
\[
x^2-x-1=0
\]
という2次方程式です。
この2次方程式の解の一つが
\[
\frac{1+\sqrt{5}}{2}
\]
となっています。つまり、この2次方程式の\(x\)に\(\frac{1+\sqrt{5}}{2}\)を代入すると
\[
\Bigl(\frac{1+\sqrt{5}}{2} \Bigr)^2-\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)-1=0
\]
が成り立つのです。
中学や高校で学ぶ「2次方程式の解の公式」を使うと、\(x^2-x-1=0\)
の解の一つが\(\frac{1+\sqrt{5}}{2}\)であることを確認できます。「中学や高校の頃、数学が好きでした!」という人は、ぜひ計算してみてくださいね。
それでは、このシンプルな2次方程式や黄金比が浮かび上がってくる「フィボナッチ数列」と「黄金長方形」という不思議な二つの数学の世界を紹介していきます。
ちょっと聞きなれない言葉かもしれませんが、実はみなさんの身近なところにも隠れています。
フィボナッチ数列と黄金比
突然ですが、ここで問題です。
\[
1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ 233,\ \cdots
\]
この数列、ある規則をもって並んでいます。
さて、233の次にどんな数が来るのでしょう?
少しの間、考えてみてくださいね。

この数列には
\[
1+1=2,\ 1+2=3,\ 2+3=5,\ 3+5=8,\ 5+8=13,\ 8+13=21,\ 13+21=34,\ 21+34=55,\ \cdots
\]
という規則性が隠されています。
つまり、233の次の数は
\[
144+233=377
\]
となり、377です。
そう、この数列が「フィボナッチ数列」。数学の世界では非常に有名なんです。数の羅列だけ見ていると、ちょっとした数遊びのようにも見えますが、自然界によく出現する不思議な数列として知られています。
例えば、ヒマワリの種の螺旋の本数は、フィボナッチ数列に現れる数になっていることが多いと言われています。

また、花びらの枚数も、フィボナッチ数列に現れる数になっていることが多いと言われています。

実は、この不思議な数列と黄金比、ある関係性を持っています。
フィボナッチ数列の前後の数の比(後の数÷前の数)を、順番にとってみると、とても興味深いことが起こるのです。
フィボナッチ数列
\[
1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ 233,\ 377,\ 610,\ \cdots
\]
の前後の数の比(後の数÷前の数)をとってみると…
\[
\frac{1}{1},\ \frac{2}{1},\ \frac{3}{2},\ \frac{5}{3},\ \frac{8}{5},\ \frac{13}{8},\ \frac{21}{13},\ \frac{34}{21},\ \frac{55}{34},\ \frac{89}{55},\ \frac{144}{89},\ \frac{233}{144},\ \frac{377}{233},\ \frac{610}{377},\ \cdots
\]
これを小数にしてみると…
\begin{align*}
\frac{1}{1}&=1\\
\frac{2}{1}&=2\\
\frac{3}{2}&=1.5\\
\frac{5}{3}&=1.6666666666666\cdots\\
\frac{8}{5}&=1.6\\
\frac{13}{8}&=1.625\\
\frac{21}{13}&=1.6153846153846\cdots\\
\frac{34}{21}&=1.6190476190476\cdots\\
\frac{55}{34}&=1.6176470588235\cdots\\
\frac{89}{55}&=1.6181818181818\cdots\\
\frac{144}{89}&=1.6179775280898\cdots\\
\frac{233}{144}&=1.6180555555555\cdots\\
\frac{377}{233}&=1.6180257510729\cdots\\
\frac{610}{377}&=1.6180371352785\cdots
\end{align*}
どこかで見た値に近づいていっている気がしませんか?
そうです!黄金比に出てきた
\[
\frac{1+\sqrt{5}}{2}=1.6180339887\cdots
\]
に、かなり近い値になっていますね!
実は、これを繰り返していくと、フィボナッチ数列の前後の数の比は、\(\frac{1+\sqrt{5}}{2}\)に限りなく近づいていくことが証明されています。
少々難しい話になってしまいますが、フィボナッチの数列の「特性方程式」と呼ばれる方程式が
\[
x^2-x-1=0
\]
であり、先ほどの2次方程式と一致していることが、フィボナッチ数列と黄金比を繋げるカギになっています。
デザインで大活躍!黄金長方形
では次に、自然の世界を飛び出して、デザインの世界へと足を運んでみましょう。
Webデザインなどでよく使われている「黄金長方形」を見ていきます。
この黄金長方形には「短辺と同じ長さの辺をもつ正方形を切り取っても、残った長方形は、元の長方形と同じ比率の長方形になる」という特徴があります。
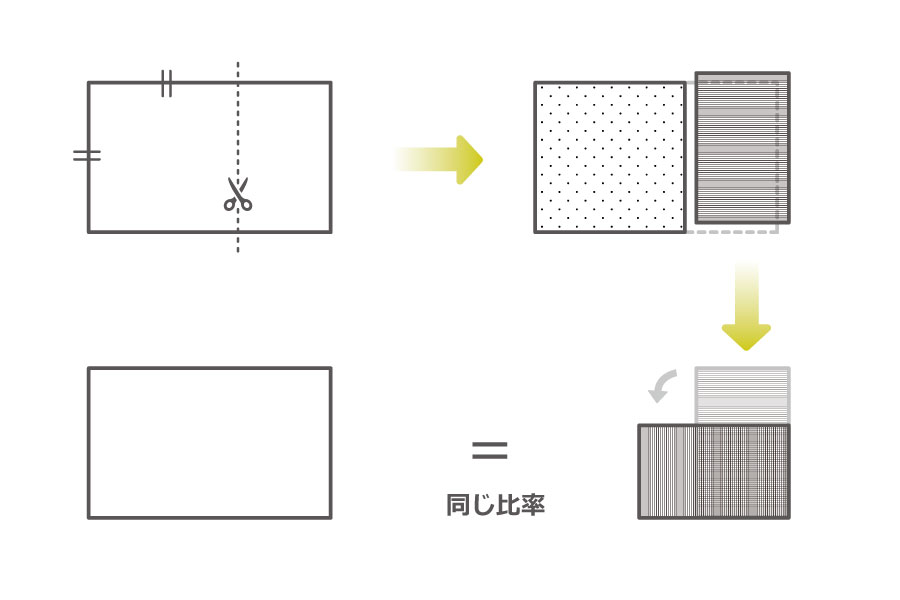
つまり、正方形を切り取り続けても、延々と同じ形の長方形が出現し続けるのです!
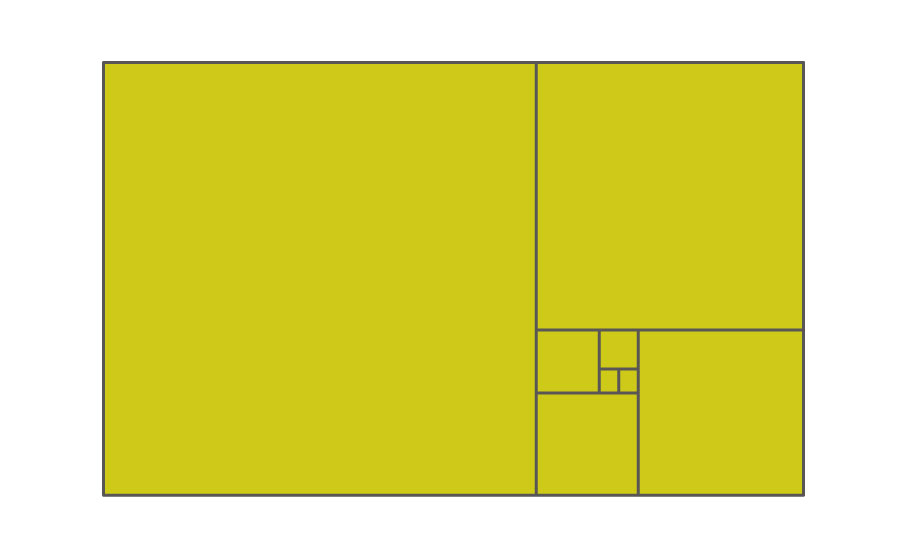
この不思議な長方形の縦横の比率を、実際に求めてみましょう。数学がどうしても苦手な方は、途中の数式部分を読み飛ばして「つまり、黄金長方形の縦横の比率は…」のところから読んでみてくださいね。
まず、短辺の長さを\(1\)、長辺の長さを\(x\)とします。

この長方形から、短辺と同じ長さの辺をもつ正方形を切り取ってみます。
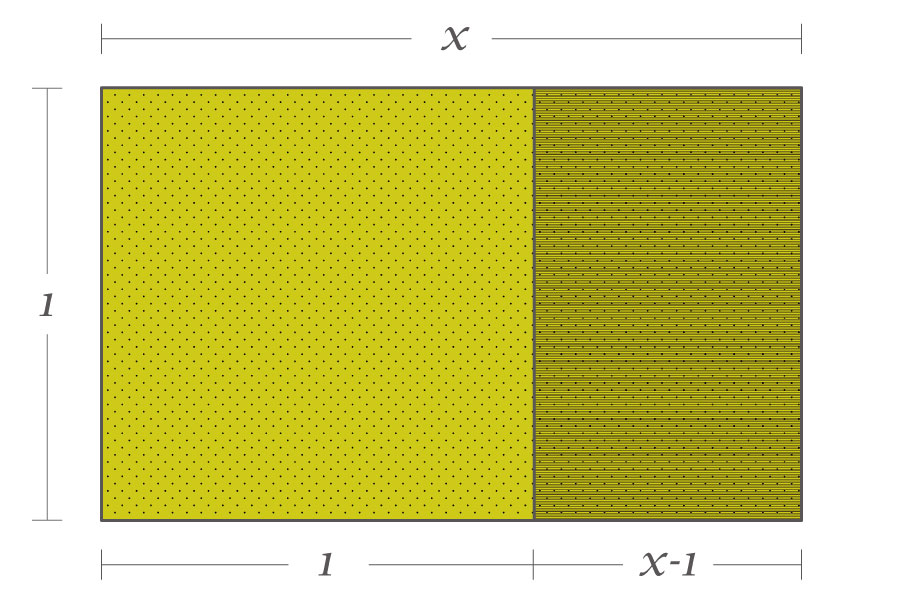
残った長方形の短辺の長さは\(x-1\)、長辺の長さは\(1\)となります。
元の長方形と残った長方形の縦横の比率は同じなので、「短辺:長辺」は変わりません。このことを式にしてみると
\[
1:x=(x-1):1
\]
となります。ここで、「内項の積=外項の積」を計算してみると…
\[
x(x-1)=1
\]
となります。この式を変形していくと…
\[
x^2-x=1
\]
\[
x^2-x-1=0
\]
となり、最初に紹介した2次方程式が出てきました!
求めたい\(x\)(元の長方形の長辺の長さ)は、この2次方程式の解です。中学や高校で習った「2次方程式の解の公式」を使って、方程式を解いてみると…
\[
x=\frac{1+\sqrt{5}}{2},\frac{1-\sqrt{5}}{2}
\]
の二つが、解となることがわかります。しかし、\(\frac{1-\sqrt{5}}{2}\)は負の値となってしまうため、長さとして適していません。
よって、
\[
\frac{1+\sqrt{5}}{2}
\]
こそが、元の長方形の長辺の長さとなります。
つまり、黄金長方形の縦横の比率は、黄金比
\[
1:\frac{1+\sqrt{5}}{2}
\]
だったのです!
では、この章の最後に、黄金長方形の中に現れる正方形の頂点を、円を描くように繋いでみましょう。すると…
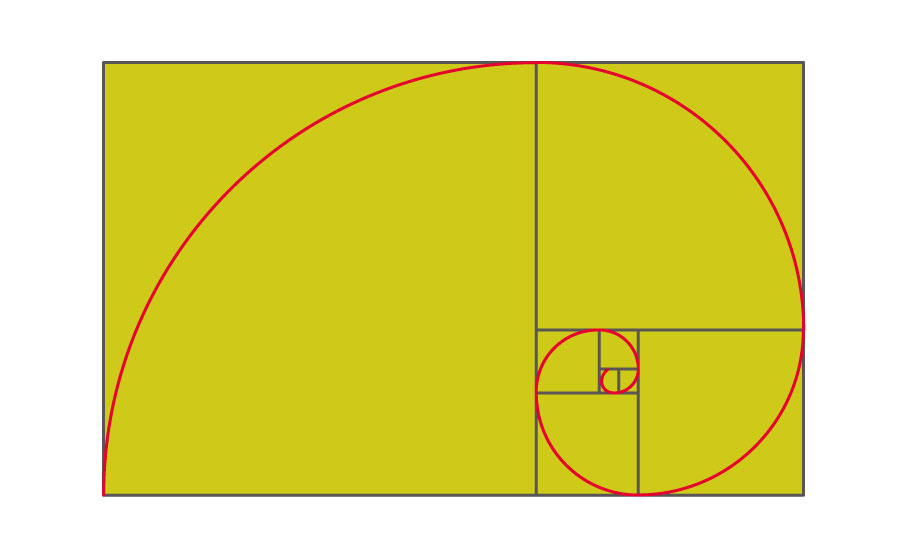
あの有名な「黄金螺旋」が出現しました!こんな仕組みになっていたんですね。
フィボナッチ数列と黄金長方形の不思議な関係
実は、この黄金長方形、フィボナッチ数列とも関わっています。
フィボナッチ数列に現れる数の辺の長さを持つ正方形を、以下のように敷き詰めてみると…
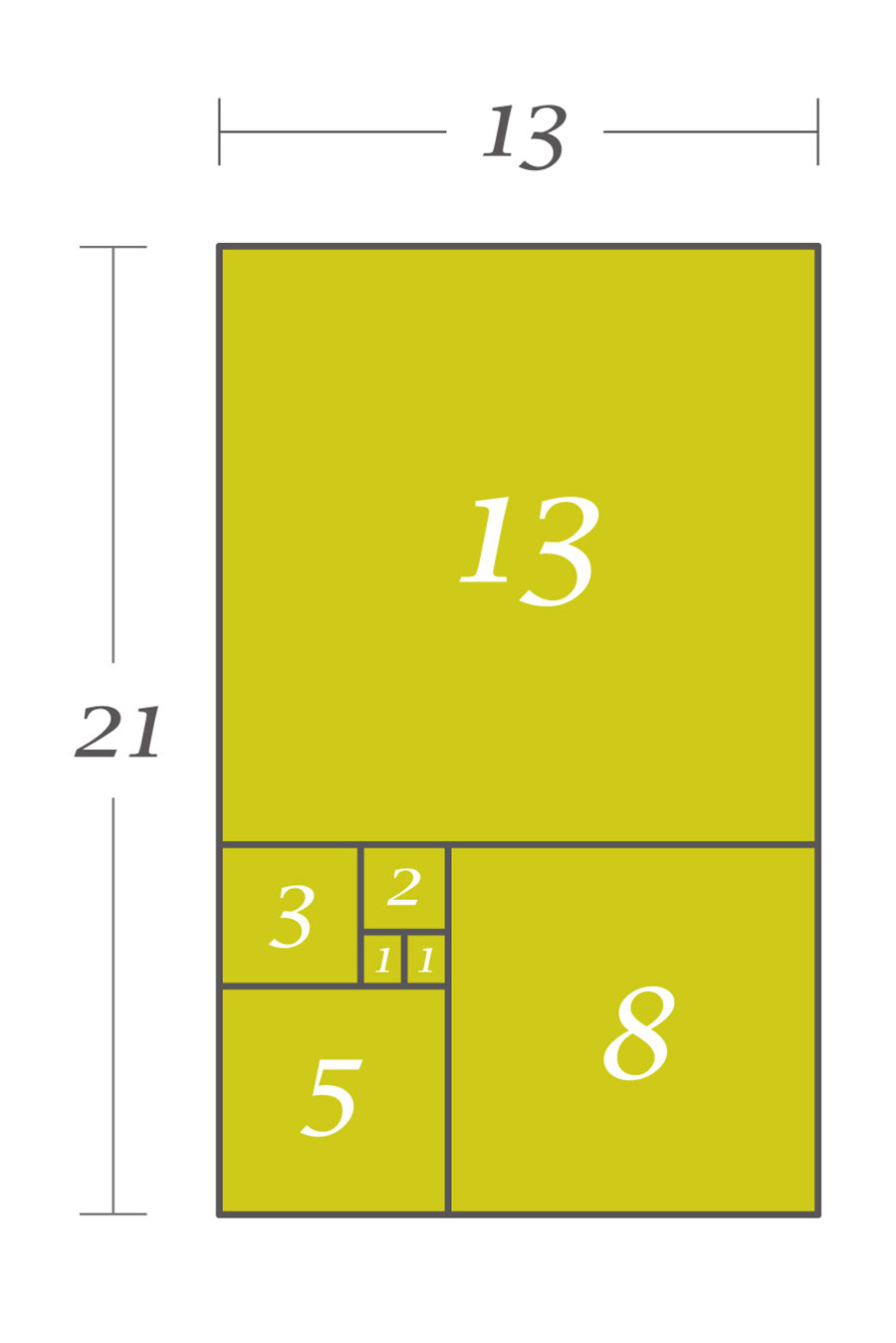
となり、この長方形の長辺÷短辺の比率は、
\[
\frac{13+8}{13}=\frac{21}{13}= 1.6153846153846\cdots
\]
となります。さらに、もう一つ敷きつめてみると…
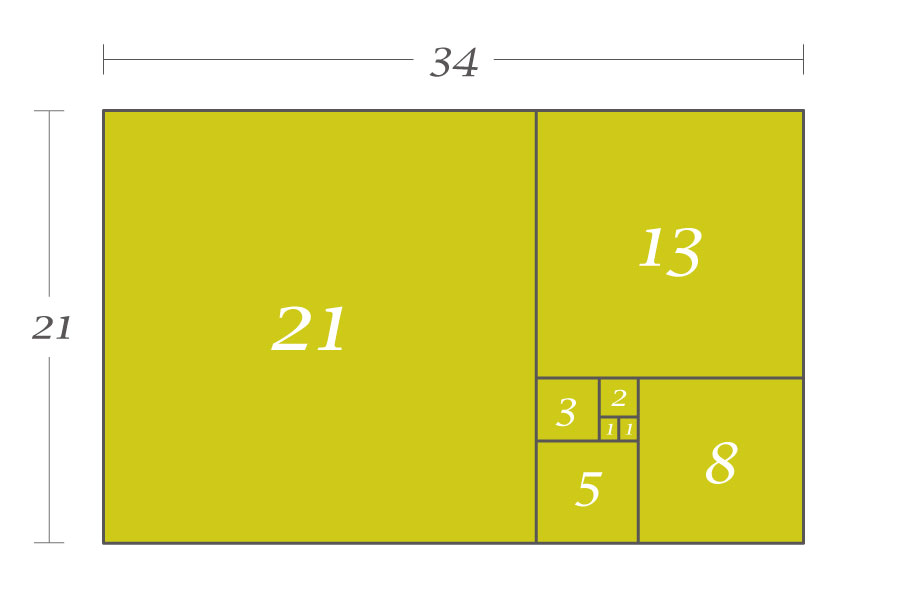
となり、この長方形の長辺÷短辺の比率は、
\[
\frac{21+13}{21}=\frac{34}{21}=1.619047619047\cdots
\]
となります。これは、先ほど見た「フィボナッチ数列の前後の数の比」になっていますよね。
ということは、このように正方形を敷きつめていく操作を延々と続けて行くと、長方形の長辺÷短辺は\(\frac{1+\sqrt{5}}{2}\)
へ限りなく近づいていきます。つまり、黄金長方形へ限りなく近づいていくのです!
また、先ほどのように、フィボナッチ数列に現れる数の辺の長さを持つ正方形からも螺旋をつくることができます。
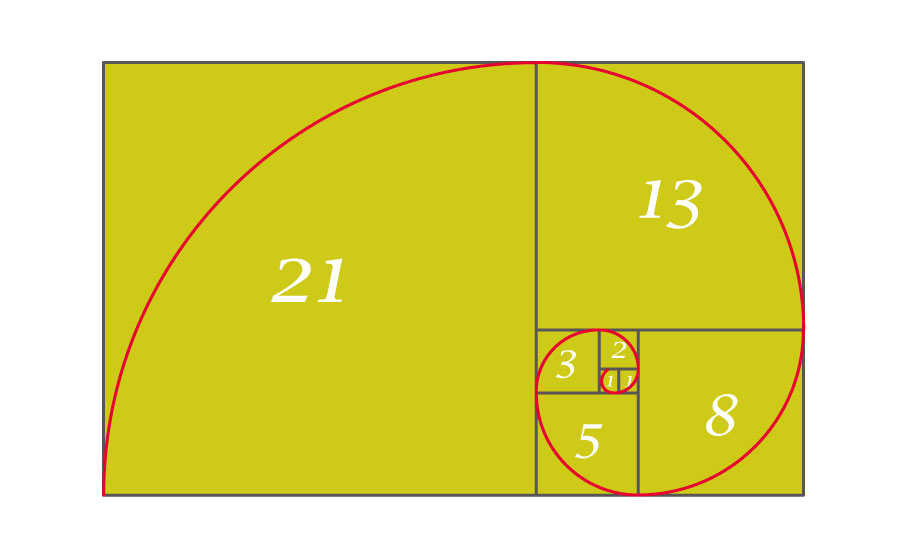
実は、今回紹介した内容は、黄金比の性質のほんの一部。まだまだ不思議で興味深い性質がたくさん隠されています。
そして、きっと、あなたの身近にも黄金比は潜んでいますよ。ぜひ、探してみて下さいね!
〈補足〉
黄金比の美しさ、黄金比が古代の美術品に出現すること、フィボナッチ数列と自然界の関連性については、諸説あります。「後付けではないか」といった意見があるものもありますが、本記事では、一般的によく知られているトピックを紹介しました。