普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。

今回は、「紙」にまつわる数学を紹介します。

書類はA4サイズ、婚姻届はA3サイズ、ノートはB5サイズ…私たちの生活に欠かせない紙のサイズ「A判・B判」。実際に、紙の長さを計ってみたことはありますか？

例えば、A4は21.0cm×29.7cmで、B5は18.2cm×25.7cmです。

何とも中途半端な長さだと思いませんか？A4は20cm×30cm、B5は20cm×25cmにしてしまった方がわかりやすそうですよね。しかし、この中途半端な長さには、数学的で合理的な秘密が隠されているのです！

無駄がない！サイズ同士の美しい関係性

A判にはA0、A1、A2、A3、A4、A5…と様々なサイズが存在しています。実は、A判のそれぞれのサイズ同士には、ある一定の関係性があるのです。

例えば、A4の紙２枚の長辺を合わせて、２倍の大きさの紙をつくってみます。

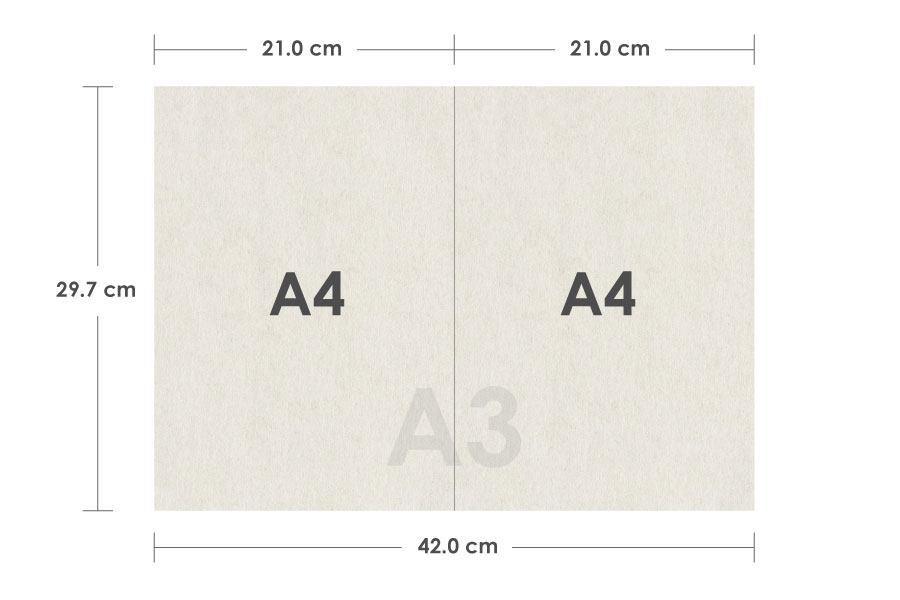
そうすると、この紙がちょうどA3になるのです。逆に言えば、A3の半分がA4ということになっています。

この関係性は「A0とA1」、「A1とA2」、「A2とA3」・・・と、どの組合せに対しても成り立っています。つまり、A0の半分はA1、A1の半分はA2、A2の半分はA3、A3の半分はA4…という関係性になっているのです。

例えば、A3・A4・A5の関係性を図にしてみると、下のようになります。

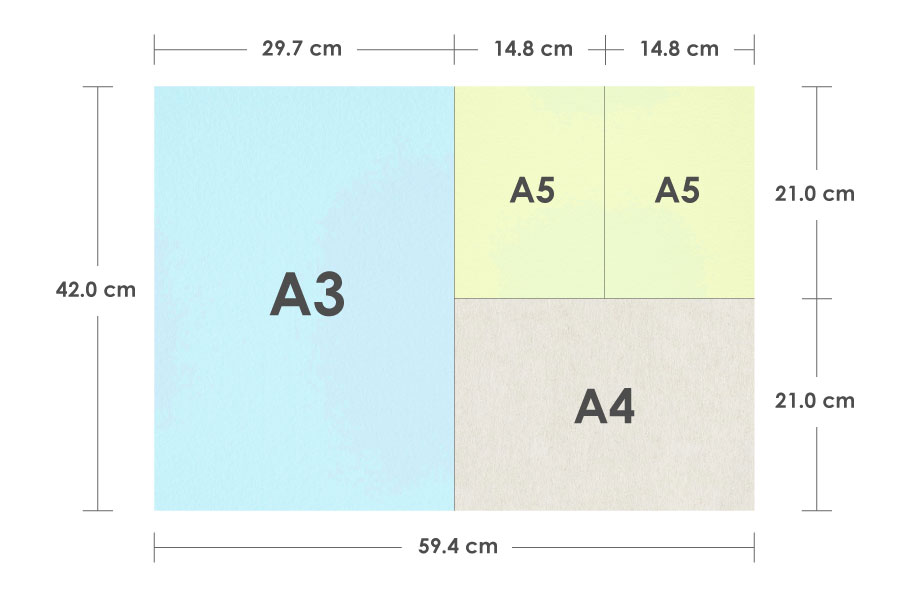
上の図の右側のように、A5の紙２枚とA4の紙１枚を組み合わせてみると、おおよそA3の大きさになります。

では、このような関係性が成り立っていることに、一体どんなメリットがあるのでしょうか？

それは「裁断のときに無駄がないこと」です。

例えば、1枚のA2の紙から、1枚のA4の紙を作る場合を考えてみましょう。まず、A2の紙を半分に裁断します。そうすると、A3の紙が２枚できます。

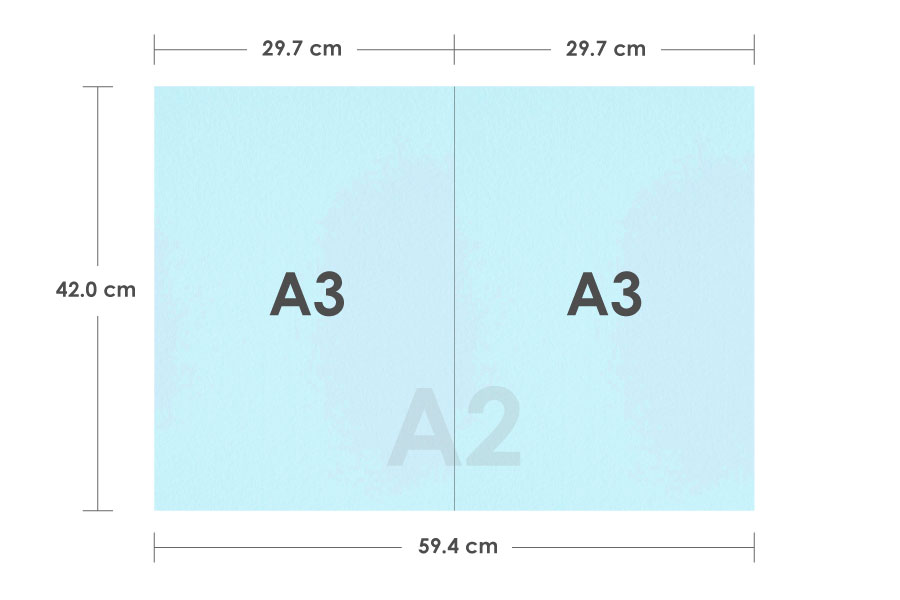
このA3の紙の１枚を、半分に裁断します。そうすると、A4の紙が２枚できます。

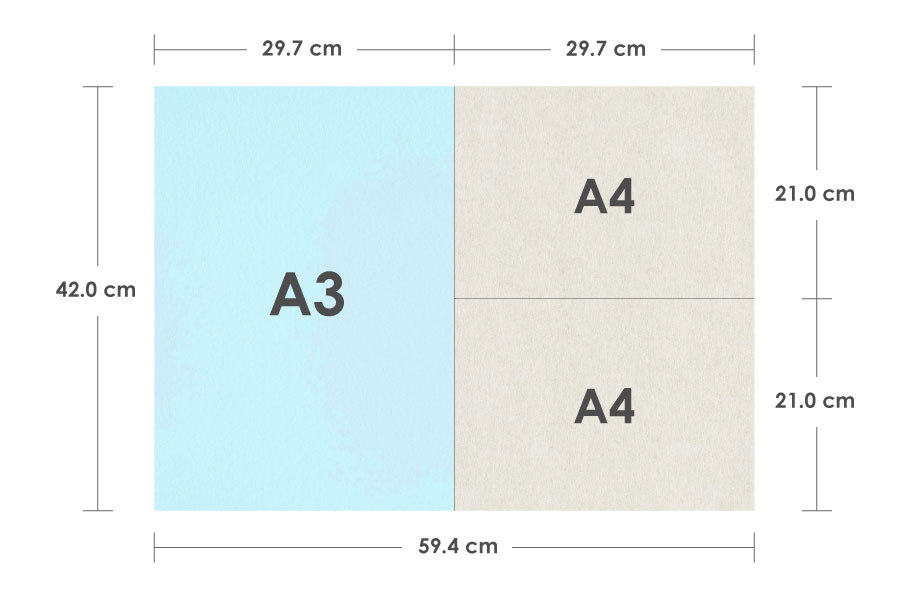
作りたかったのは、A4の紙1枚だけではありますが、裁断の際に残ってしまったA3の紙１枚、A4の紙1枚も「A判の紙」として活用することができますよね。つまり、無駄がないのです。

この関係性はB判についても、同じように成り立っています。

比率は、黄金比ならぬ「白銀比」

実は、A判・B判どちらも「全ての紙の縦横の比率が同じ」という秘密が隠されています。

そのため、A判・B判の中には、妙に細長～い長方形が存在する…なんてことはありません。A0もA1もA2もA3もA4も全て同じ縦横の比率。大きさは違いますが、全て同じ形状の長方形です。

大きさは違うけれど同じ形状…つまり、マトリョーシカのようになっているのです！

さらに、先ほどの話と合わせると、「紙を半分に裁断しても縦横の比率は変わらない」ということになります。

この不思議な比率…一体、具体的にはどんな数の比なのでしょうか？

中学校で習った数学を思い出して、実際に求めてみましょう。数学がどうしても苦手な方は、数式の部分を読み飛ばして、「そう！」の後から読んでみてくださいね。

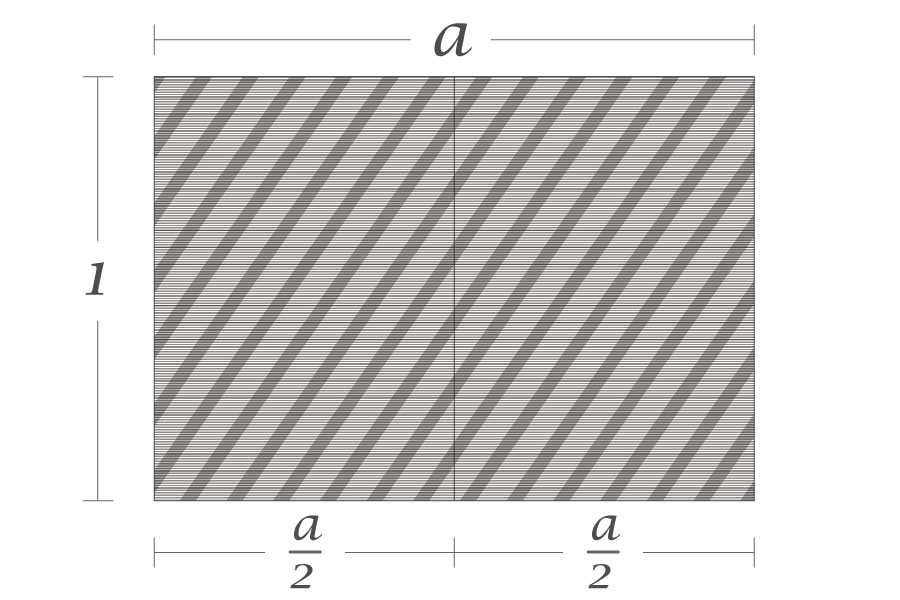
元の紙のサイズの短辺を1、長辺を\(a\)とおきます。この紙を半分に裁断すると、短辺が\(\frac{a}{2}\)、長辺が1となります。比率が変わらないということは、「短辺:長辺」が変わらないということ。つまり

\[
1:a=\frac{a}{2}:1
\]

が成り立っているということですよね。ここで、「内項の積=外項の積」を使ってみると

\[
a\times\frac{a}{2}=1\times1
\]

となります。両辺を2倍してみると・・・

\[
a^2 = 2
\]

という式が出てきます。「2乗すると、2になる数」って、記憶の片隅にありませんか？

そう！「\(\sqrt{2}\)」です。つまり、A判やB判サイズの紙の比は、「\(1:\sqrt{2}\)」になっているのです。

実は、この「\(\sqrt{2}\)」、ちょっとクセモノで

\[
\sqrt{2}=1.41421356\cdots
\]

となっており、キリの良い数ではありません。そのため、実際の紙の長さにしたときに、どうしても中途半端な長さになってしまうのです。

この「\(1:\sqrt{2}\)」の比は「白銀比」や「大和比」と呼ばれており、日本古来の建築でも使われていると言われている、とっても便利で美しい比です。

私たちの身近なものに、実は深～い数学が隠されているんですね！